Time limit: 0
Finish Test
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
- Most Important Multiple Choice Questions
- Online Pipes and Cisterns Exercise with Correct Answer Key and Solutions
- Useful for all Competitive Exams
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
- Question 1 of 20
1. Question
Two taps can fill a tank in 12 and 18 minutes respectively. Both are kept open for 2 minutes and the first is turned off. In how many minutes more will the tank be filled?
Hint
Part filled by first tap in 1 min
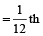
Part filled by second tap in 1 min
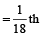
Now,
since
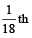part of tank is filled by second tap in 1min.∴
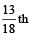part of tank is filled by second tap in 1 min.
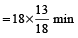= 13 min. - Question 2 of 20
2. Question
Two pipes A and B can fill a cistern in 10 and 15 minutes respectively. Both fill pipes are opened together, but at the end of 3 minutes, ‘B’ is turned off. How much time will the cistern take to fill?
Hint
In one min, (A + B) fill the cistern
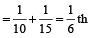
In 3 min, (A + B) fill the cistern
=
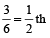
Remaining part
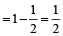
since
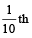part filled by A in one min.∴ ½nd part filled by A in 10 × ½ = 5 minutes
∴ Total time = 3 + 5 = 8 min.
- Question 3 of 20
3. Question
Two fill pipes A and B can fill a cistern in 12 and 16 minutes respectively. Both fill pipes are opened together, but 4 minutes before the cistern is full, one pipe A is closed. How much time will the cistern take to fill?
Hint
Let cistern will be full in x min. Then,
part filled by B in x min + part filled by A in
(x – 4) min = 1
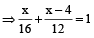
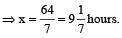
- Question 4 of 20
4. Question
Two fill taps A and B can separately fill a cistern in 45 and 40 minutes respectively. They started to fill a cistern together but tap A is turned off after few minutes and tap B fills the rest part of cistern in 23 minutes. After how many minutes, was tap A turned-off?
Hint
Let A was turned off after x min. Then,
cistern filled by A in x min + cistern filled by B in
(x + 23) min = 1
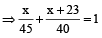
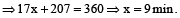
- Question 5 of 20
5. Question
Three fill pipes A, B and C can fill separately a cistern in 3, 4 and 6 minutes respectively. A was opened first. After 1 minute, B was opened and after 2 minutes from the start of A, C was also opened. Find the time when the cistern will be full?
Hint
Let cistern will be full in x min. Then,
part filled by A in x min + part filled by B in
(x – 1) min + part filled by c in (x – 2)min = 1
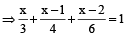
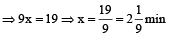
- Question 6 of 20
6. Question
Three taps A, B and C can fill a tank in 12, 15 and 20 hours respectively. If A is open all the time and B and C are open for one hour each alternately, then the tank will be full in:
Hint
(A + B)’s 1 hour’s work
=
(A + C)’s 1 hour’s work
=
Part filled in 2 hrs
=
Part filled in 6 hrs
=
Remaining part
=
Now, it is the turn of A and B and 3/20 part is filled by A and B in 1 hour.
∴ Total time taken to fill the tank
= (6 + 1) hrs = 7 hrs.
- Question 7 of 20
7. Question
A hot pipe takes 3 minutes longer to fill a tank than the cold pipe. Together they take 6 minutes 40 seconds. Time taken by the cold pipe alone to fill the tank is :
Hint
Let cold pipe take X minutes, then hot pipe will take (X + 3) minutes.
Together
=
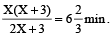
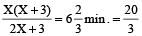
40X + 60 = 3X (X + 3)
⇒ 40X + 60 = 3X² + 9X
⇒ 3X² – 31X – 60 = 0
⇒ X = 12 minutes
- Question 8 of 20
8. Question
Two pipes P and Q would filled a cistern in 24 hours and 32 hours respectively . If both pipes are opened together, find when the first pipe must be turned off so that the cistern may be just filled in 16 hours?
Hint
Suppose the first pipe was closed after x hrs.
Then, first’s x hrs supply + second’s 16 hrs supply = 1
or,
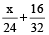=1∴
= 1 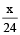– ½= ½∴ x = 12 hrs.
Quicker method :
The first pipe should work for
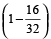× 24 hrs.= 12hrs
- Question 9 of 20
9. Question
If two pipes function simultaneously, the reservoir is filled in 12 hrs. One pipe fills the reservoir 10 hrs faster than the other .How many hours does the faster pipe take to fill the reservoir?
Hint
Let the faster pipe fills the tank in x hrs.
Then the slower pipe fills the tank in x + 10 hrs.
When both of then are opened, the reservoir will be filled in
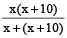= 12⇒ x² – 14x – 120 = 0
∴ x = 20, – 6
But x can’t be – ve, hence the faster pipe will fill the reservoir in 20 hrs.
- Question 10 of 20
10. Question
A cistern has two taps (which fill it in 12 min and 15 min, respectively) and an exhaust tap. When all three taps are opened together, it takes 20 min to fill the empty cistern. How long will the exhaust tap take to empty it?
Hint
Let the exhaust tap empties the tank in x minutes.
Then,
⇒
⇒
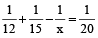
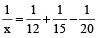
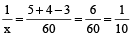
⇒ x = 10 min
- Question 11 of 20
11. Question
One tap can fill a cistern in 2 hours and another can empty the cistern in 3 hours. How long will they take to fill the cistern if both the taps are open?
Hint
Work of both tap for 1 hour
=
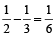
Hence, both tap will fill the cistern in 6 hours.
- Question 12 of 20
12. Question
Two pipes can fill a tank in 20 and 24 minutes respectively and a waste pipe can empty 3 gallons per minute. All the three pipes working together can fill the tank in 15 minutes. The capacity of the tank is :
Hint
Work done by the waste pipe in 1 minute
=
[–ve sign means emptying]∴ Volume of ¹⁄₄₀ part
= 3 gallons.
Volume of whole
= (3 × 40) gallons
= 120 gallons.
- Question 13 of 20
13. Question
Tap ‘A’ can fill a water tank in 25 minutes, tap ‘B’ can fill the same tank in 40 minutes and tap ‘C’ can empty that tank in 30 minutes. If all the three taps are opened together, in how many minutes will the tank be completely filled up or emptied?
Hint
Tank filled in 1 minute
=
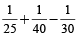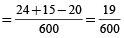part
part∴ tank will be filled complete in minutes
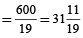
- Question 14 of 20
14. Question
A water tank is ⅖th full. Pipe A can fill the tank in 10 minutes and the pipe B can empty it in 6 minutes. If both the pipes are open, how long will it take to empty or fill the tank completely?
Hint
Since pipe A in 1 minute fills ¹⁄₁₀ part and Pipe B in 1 min. empties ⅙ part
∴ Pipe A + B in 1 min
=
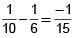
Since ¹⁄₁₅ part gets emptied in 1 min
∴ ⅖ part is emptied in
15 × ⅖ min = 6 min
- Question 15 of 20
15. Question
A tap can fill a tank in 16 minutes and another can empty it in 8 minutes. If the tank is already 1/2 full and both the taps are opened together, will the tank be filled or emptied? How long will it take before the tank is either filled or emptied completely as the case may be?
Hint
If both the pumps are opened together, then the tank will be emptied because the working efficiency of pump emptying is more than that of the pump filling it. Thus in 1 min net work done
=
partsor the tank will be emptied in 16 min
⇒ ½ tank will be emptied in 8 min.
- Question 16 of 20
16. Question
A pipe can fill a tank in 15 minutes and another one in 10 minutes. A third pipe can empty the tank in 5 minutes. The first two pipes are kept open for 4 minutes in the beginning and then the third pipe is also opened. In what time will the tank be emptied?
Hint
Proportion of the volume of the tank filled by both the pipes in 4 min
=
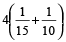
= ⅔rd of the tank.
Volume of the tank filled by all the pipes working together
=
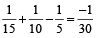
i.e. 1/30 tank is emptied in 1 min.
- Question 17 of 20
17. Question
Pipes A and B can fill a tank in 5 and 6 hours respectively. Pipe C can empty it in 12 hours. If all the three pipes are opened together, then the tank will be filled in:
Hint
Net part filled in 1 hour
=
.∴ The tank will be full in
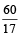hrsi.e.,
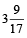hrs. - Question 18 of 20
18. Question
A, B, C are pipes attached to a cistern. A and B can fill it in 20 and 30 minutes, respectively, while C can empty it in 15 minutes, If A, B and C be kept open successively for 1 minute each, how soon will the cistern be filled?
Hint
1 minute’s work of each of the three pipes
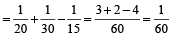
i.e., work of 3 pipes for 3 minutes
=
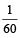
∴ Work of 3 pipes for 55 minutes each
=
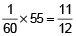
∴ Remaining part to be filled
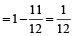
Now, pipe A will fill 1/20 of the cistern in next 1 minute.
∴ Remaining portion to be filled by pipe B
=
– 
=
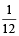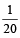
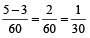
∴ Time taken by pipe B to fill 1/30 of the cistern = 1/30 × 30 = 1min
Hence, total time
= (55 × 3) + 1 + 1
= 167 min.
- Question 19 of 20
19. Question
Six pipes are fitted to a water tank. Some of these are inlet pipes and the others outlet pipes, Each inlet pipe can fill the tank in 9 hours and each outlet pipe can empty the tank in 6 hours. On opening all the pipes, an empty tank is filled in 9 hours. The number of inlet pipes is
Hint
Total number of pipes = 6 (given)
Let number of inlet pipes = x
∴ number of outlet pipes = 6 –x
Now, Inlet pipe fill the tank in 9 hours and outlet pipe empty it in 6 hours.
∴ Total part filled in 1 hour
=
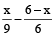
When all the pipes are opened.
But given total part filled in 9 hr
∴
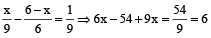
⇒ 15x = 60 ⇒ x = 4
Hence, number of inlet pipes = 4.
- Question 20 of 20
20. Question
Two pipes A and B can fill a tank in 15 hours and 20 hours respectively while a third pipe C can empty the full tank in 25 hours. All the three pipes are opened in the beginning. After 10 hours, C is closed. In how much time, will the tank be full?
Hint
Part filled in 10 hours
=
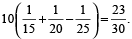
Remaining part
=
(A + B)’s 1 hour’s work
=
⇒
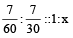
∴ The tank will be full in (10 + 2) hrs = 12 hrs.