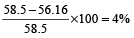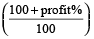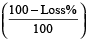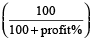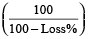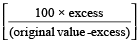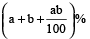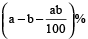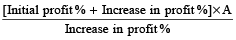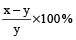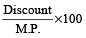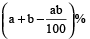Cost Price: The amount paid to purchase an article or the price at which an article is made, is known as its cost price. The cost price is abbreviated as C.P..
Selling Price: The price at which an article is sold, is known as its selling price. The selling price is abbreviated as S.P.
Profit: If the selling price (S.P.) of an article is greater than the cost price (C.P.) , then the difference between the selling price and cost price is called profit.
Thus, If S.P. > C.P., then
Profit = S.P. – C.P.
⇒ S.P. = C.P. + Profit
⇒ C.P. = S.P. – Profit.
Example 1: A shopkeeper buys scientific calculators in bulk for Rs. 15 each. He sells them for Rs. 40 each. Calculate the profit on each calculator in rupees, and as a percentage of the cost price.
Solution: Given: cost price = Rs. 15, selling price = Rs. 40
Profit = selling price – cost price = Rs. 40 – 15 = Rs. 25
the profit as a percentage of the cost price:
Profit % =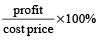 
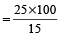% = 166.7%
Loss: If the selling price (S.P.) of an article is less than the cost price (C.P.) , then the difference between the cost price (C.P.) and the selling price (S.P.) is called loss.
Thus, if S.P. < C.P., thenLoss = C.P. – S.P.⇒ C.P. = S.P. + Loss⇒ S.P. = C.P. – Loss [/av_textblock][av_textblock size='' av-medium-font-size='' av-small-font-size='' av-mini-font-size='' font_color='' color='' id='' custom_class='ed-text-block-sm-textp' av_uid='av-2wpi6q4-1' admin_preview_bg=''] Example 2: If the cost price of a book is Rs. 150 and selling price is 137.50, then calculate the loss and percentage loss on the book?
Solution: Here, cost price = Rs. 150
and selling price = Rs. 137.50
∴Loss = Cost price – selling price
= Rs. (150 – 137.50) = Rs. 12.50
Now, Percentage Loss
= 
%
= 
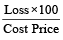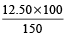% = 8.33%
Quicker Method to solve the questions
When cost price and percentage profit are given, then selling price
= cost price
Example 3: A chair was purchased for Rs. 470 and sold at a profit of 10%. Find the selling price.
Solution: Using the formula
Selling price = cost price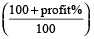 
= 470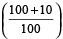
= 
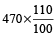= Rs. 517
When cost price and percentage loss are given, then
Selling price = cost price
Example 4: A person bought a table for Rs. 420 and sold at the loss of 15% . Find the selling price of table?
Solution: Selling price = cost price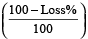 
= Rs. 420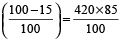 
= Rs. 357
When selling price and percentage profit are given, then
Cost price = selling price
Example 5: A Chair was sold for Rs. 517 at a profit of 10%. Find the cost price of the chair.
Solution: Here, selling price = Rs. 517 and profit = 10%
∴ Cost price = selling price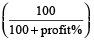 
= 
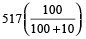
= 517 ×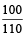 
= Rs. 470
When selling price and percentage loss are given, then
Cost price = selling price
Example 6: Ram sold a watch for Rs. 376 at a loss of 6%. Find the cost price of the watch.
Solution:
Cost price = selling price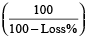 
= Rs. 376 ×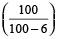 
= Rs. 376 ×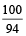 
= Rs. 400
If two items are sold each at rupees R, one at a gain of x% and other at a loss of x %, there is always an overall loss given by
% and the value of loss is given by
.
In case the cost price of both the items is the same and percentage loss and gain are equal, then net loss or profit is zero. The difference between the two cases is that the cost price in the first case is not the same, and in the second case it is the same.
Example 7: Ram sells two Mobile phones for Rs. 1000 each, one at a profit of 10% and other at a loss of 10%. Find his gain or loss percentage.
Solution: Using the formula,
Loss % = 
% = 1%
A dishonest shopkeeper claims to sell goods at cost price, but uses a lighter weight, then his Gain %
=
Example 8: A shopkeeper sells rice to a customer, using false weights and gains 100/8 % on his cost. What weight has he substituted for a kilogram?
Solution: Using the formula,
Gain % =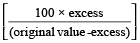 
From here, Excess = 0.111.. Kg, which is 111.11 grams
Weight used by shopkeeper = 1000 – 111.11 = 888.89 grams
Formulas to Remember
Profit =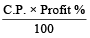 
Loss =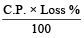 
S.P. =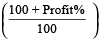 
× C.P.
S.P. =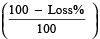 
× C.P.
C.P. =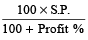 
C.P. =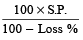 
Goods passing through successive hands
When there are two successive profits of a% and b%, then the resultant profit per cent is given by
When there is a profit of a% and loss by b% in a transaction, then the resultant profit or loss per cent is given by
according to the +ve or –ve sign respectively.
When cost price and selling price are reduced by the same amount (A) and profit increases then cost price (C.P.)
=
Example 9: A table is sold at a profit of 20%. If the cost price and selling price are Rs. 200 less, the profit would be 8% more. Find the cost price.
Solution: By direct method,
C.P. =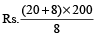 
= Rs. 28 × 25 = Rs. 700.
If cost price of x articles is equal to the selling price of y articles, then profit/loss percentage
=
according to +ve or –ve sign respectively.
Example 10: If the C.P. of 15 tables be equal to the S.P. of 20 tables, find the loss per cent.
Solution: By direct method,
Profit/Loss % =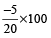 
= –25% loss, since it is –ve.
Discount
The reduction made on the ‘marked price’ of an article is called the discount. When no discount is given, ‘selling price’ is the same as ‘marked price’.
Discount = Marked price × Rate of discount.
S.P. = M.P. – Discount.
Discount % =
Example 11: How much % must be added to the cost price of goods so that a profit of 20% must be made after throwing off a discount of 10% from the marked price?
Solution: (c) Let C.P. = Rs. 100, then S.P. = Rs. 120
Also, Let marked price be Rs. x. Then, 90% of x = 120
⇒ 
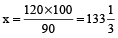
∴ M.P. should be Rs.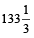 
or M.P. =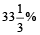 
above C.P.
Buy x get y free i.e., if x + y articles are sold at cost price of x articles, then the percentage discount
=
× 100.
Successive Discounts
In successive discounts, first discount is subtracted from the marked price to get net price after the first discount. Taking this price as the new marked price, the second discount is calculated and it is subtracted from it to get net price after the second discount. Continuing in this manner, we finally obtain the net selling price.
In case of successive discounts a% and b%, the effective discount is:
Example 12: Find the single discount equivalent to successive discounts of 15% and 20%.
Solution: By direct formula,
Single discount
= 
= 
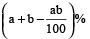
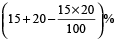
= 32 %
If the list price of an item is given and discounts d₁and d₂ are given successively on it then, Final price = list price
Example 13: An article is listed at Rs. 65. A customer bought this article for Rs. 56.16 and got two successive discounts of which the first one is 10%. The other rate of discount of this scheme that was allowed by the shopkeeper was :
- 3%
- 4%
- 6%
- 2%
Solution: (2): Price of the article after first discount = 65 – 6.5 = Rs. 58.5
Therefore, the second discount
= 