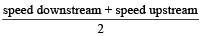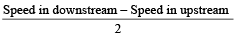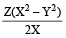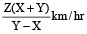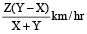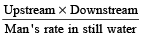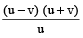- Stream: It implies that the water in the river is moving or flowing.
- Upstream: Going against the flow of the river.
- Downstream: Going with the flow of the river.
- Still water: It implies that the speed of water is zero (generally, in a lake) .
When we move upstream, our speed gets deducted from the speed of the stream. Similarly when we move downstream our speed gets added.
Let the speed of a boat in still water be A km/hr and the speed of the stream (or current) be B km/hr, then
- Speed of boat with the stream = (A + B) km/hr
- Speed of boat against the stream = (A – B) km/hr
- Speed of boat in still water is:
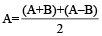
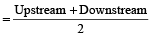
- Speed of the stream or current is:
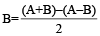
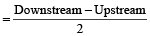
Quicker Method to solve the Questions
Boat’s speed in still water
=
Example 1: A boat travels equal distance upstream and downstream. The upstream speed of boat was 10 km/hr, whereas the downstream speed is 20 km/hr. What is the speed of the boat in still water?
Solution: Upstream speed = 10 km/hr
Downstream speed = 20 km/hr
As per formula, Boat’s speed in still water
= 
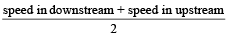
Therefore, Boat’s speed in still water
= 
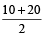= 15
Speed of current
=
Example 2: A boat travels equal distance upstream and downstream. The upstream speed of boat is 10 km/hr, whereas the downstream speed is 20 km/hr. What is the speed of the current?
Solution: Upstream speed = 10 km/hr
Downstream speed = 20 km/hr
As per formula, Speed of current
=
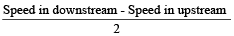
Therefore, Speed of current
= 
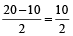= 5 km/hr
Example 3: A boat is rowed down a river 28 km in 4 hours and up a river 12 km in 6 hours. Find the speed of the boat and the river.
Solution: Downstream speed is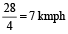 
,
Upstream speed is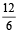 
= 2 kmph
Speed of Boat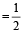 
(Downstream + Upstream Speed)
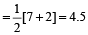kmph
Speed of current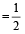 
(Downstream–Upstream speed)
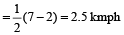
A man can row X km/h in still water. If in a stream which is flowing of Y km/h, it takes him Z hours to row to a place and back, the distance between the two places is
Example 4: A man can row 6 km/h in still water. When the river is running at 1.2 km/h, it takes him 1 hour to row to a place and back. How far is the place?
Solution: Man’s rate downstream = (6 + 1.2) = 7.2 km/h.
Man’s rate upstream = (6 – 1.2) km/h = 4.8 km/h.
Let the required distance be x km.
Then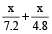 
= 1
or 4.8x + 7.2x = 7.2 × 4.8
⇒ 
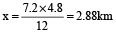
By direct formula:
Required distance
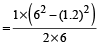
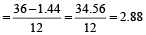km
A man rows a certain distance downstream in X hours and returns the same distance in Y hours. If the stream flows at the rate of Z km/h, then the speed of the man in still water is given by
And if speed of man in still water is Z km/h then the speed of stream is given by
Example 5: Vikas can row a certain distance downstream in 6 hours and return the same distance in 9 hours. If the stream flows at the rate of 3 km/h, find the speed of Vikas in still water.
Solution: By the formula,
Vikas’s speed in still water
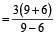= 15 km/h
If a man capable of rowing at the speed u of m/sec in still water, rows the same distance up and down a stream flowing at a rate of v m/sec, then his average speed through the journey is
=
=
Example 6: Two ferries start at the same time from opposite sides of a river, travelling across the water on routes at right angles to the shores. Each boat travels at a constant speed though their speeds are different. They pass each other at a point 720 m from the nearer shore. Both boats remain at their sides for 10 minutes before starting back. On the return trip they meet at 400 m from the other shore. Find the width of the river.
Solution: Let the width of the river be x.
Let a, b be the speeds of the ferries.
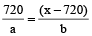… (i)
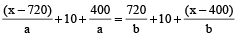… (ii)
(Time for ferry 1 to reach other shore + 10 minute wait + time to cover 400m) = Time for freely 2 to cover 720m to other shore + 10 minute wait + Time to cover (x – 400m) )
Using (i) , we get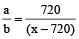 
Using (ii) ,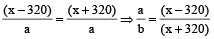 
On, solving we get, x = 1760m