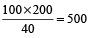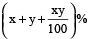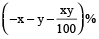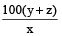Percentage is a way of expressing a number, especially a ratio, as a fraction of 100. The word is derived from the Latin per centum meaning ‘by the hundred’. It is often denoted using the percent sign, ‘%’, or the abbreviation ‘pct.’ For example, 35% (read as ‘thirty-five percent’) is equal to 35/100, or 0.35.
Quicker Methods to Solve the Problems
For converting a fraction or a decimal to a Percentage, multiply it by hundred
Example 1: Convert the fraction 3/5 into percent fraction.
Solution:  % = 60%
% = 60%
Example 2: Convert the fraction 3.5/100 into percent fraction
Solution: 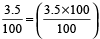 % = 3.5%
% = 3.5%
For converting a percentage to a fraction or decimal, divide by hundred.
Example 3: What is the fraction of 60%?
Solution: 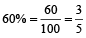
If price of a commodity is increased by x%, the consumption should be reduced, so that the expense remains the same, by
× 100%.
Example 4: If the price of sugar is increased by 25%, find how much percent a family must reduce their consumption of sugar so as not to increase the expenditure of the family?
Solution: Reduction in consumption of sugar
 % = 20%
% = 20%
If A is x % greater than B, then B will be
% lesser than A.
Example 5: If the price of Kerosene oil falls by 10%, find how much perecent can a householder increase its consumption, so as not to decrease expenditure on this item?
Solution: Increase in consumption of Kerosene oil
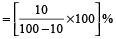
= 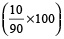 % = 11.11%
% = 11.11%
If price of a commodity is decreased by x %, the consumption can be increased, so that the expense remains the same, by
%
Example 6: If Ravi’s salary is 50% more than that of Gopal’s, then how much percent is Gopal’s salary less than that of Ravi’s salary?
Solution: Gopal’s salary is less than that of Ravi’s by
= 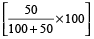 % =
% = 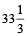 %
%
If A is x % greater than B, then B will be
% lesser than A.
Example 7: If income of Rekha is 30% less than that of Vina, then how much percent is Vina’s income more than that of Rekha?
Solution: Vina’s income is more than that of Rekha by
= 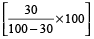 %
%
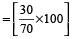 %
% 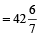 %
%
Population Formula
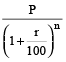
If the original population of a town is P, and the annual increase is r %, then the population after n years is
and population before n years =
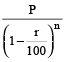
If the annual decrease be r %, then the population after n years is
and population before n years =
Example 8: The population of a certain town increased at a certain rate per cent per annum. Now it is 456976. Four years ago, it was 390625. What will it be 2 years hence?
Solution: Suppose the population increases at r% per annum.
Then,  = 456976
= 456976
∴ 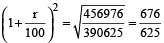
Population 2 years hence = 456976
= 456976 ×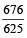 = 494265 approximately.
= 494265 approximately.
First Increase and then decrease
If the value is first increased by x % and then decreased by y% then there is
increase or decrease, according to the +ve or –ve sign respectively.
Example 9: A number is increased by 10%. and then it is decreased by 10%. Find the net increase or decrease per cent.
Solution: % change = 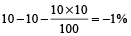
i.e., 1% decrease.
Average percentage rate of change over a period.
=
×
% [where n = period]
The percentage error =
× 100%
Successive Increase or decrease
If the value is increased successively by x % and y % then the final increase is given by
If the value is decreased successively by x % and y % then the final decrease is given by
Example 10: The price of a car is decreased by 10 % and 20 % in two successive years. What per cent of price of a car is decreased after two years?
Solution: Put x = – 10 and y = – 20, then
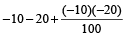 = – 28%
= – 28%
∴ The price of the car decreases by 28%.
Student and Marks
The percentage of passing marks in an examination is x%. If a candidate who scores y marks fails by z marks, then the maximum marks
M =
A candidate scoring x % in an examination fails by ‘a’ marks, while another candidate who scores y% marks gets ‘b’ marks more than the minimum required passing marks. Then the maximum marks
.
Example 11: Vishal requires 40% to pass. If he gets 185 marks, falls short by 15 marks, what was the maximum he could have got?
Solution: If Vishal has 15 marks more, he could have scored 40% marks.
Now, 15 marks more than 185 is 185 + 15 = 200
Let the maximum marks be x, then 40% of x = 200
or 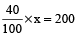
or 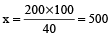
Thus, maximum marks = 500
Quicker method:
Maximum marks
=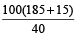
=