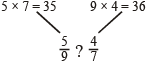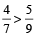A number system relates quantities and symbols. The base or radix of a number system represents the number of digits or basic symbols in that particular number system.
Decimal is a base (or radix) 10 numeral system. This means that the system has ten symbols or numerals to represent any quantity. These symbols are called Digits. The ten symbols are 1, 2, 3, 4, 5, 6, 7, 8, 9 and 0. decimal number system, also called Hindu-Arabic, or Arabic, number system, in mathematics, positional numeral system employing 10 as the base and requiring 10 different numerals.
Types of Numbers
Real numbers: Real numbers comprise the full spectrum of numbers. They can take on any form – fractions or whole numbers, decimal points or no decimal points. The full range of real numbers includes decimals that can go on forever and ever without end.
For Example: 8, 6, 2 + 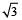 , 3/5 etc.
, 3/5 etc.
Natural numbers: A natural number is a number that comes naturally. Natural Numbers are counting numbers from 1, 2, 3, 4, 5, ……..
Whole numbers: hole numbers are just all the natural numbers plus zero.
For Example: 0, 1, 2, 3, 4, 5, and so on upto infinity.
Integers: Integers incorporate all the qualities of whole numbers and their opposites (or additive inverses of the whole numbers) . Integers can be described as being positive and negative whole numbers.
For Example: … –3, –2, –1, 0, 1, 2, 3, . . .
Rational Numbers: All numbers of the form p/q where p and q are integers (q ≠ 0) called Rational numbers.
For Example: 4, 3/4, 0, ….
Irrational Numbers: Irrational numbers are the opposite of rational numbers. An irrational number cannot be written as a fraction, and decimal values for irrational numbers never end and do not have a repeating pattern in them. ‘pi’ with its never-ending decimal places, is irrational.
For Example: 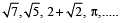
Even Numbers: An even number is one that can be divided evenly by two leaving no remainder, such as 2, 4, 6, and 8.
Odd Numbers: An odd number is one that does not divide evenly by two, such as 1, 3, 5, and 7.
Prime Number: A prime number is a number which can be divided only by 1 and itself. The prime number has only two factors, 1 and itself.
For example: 2, 3, 7, 11, 13, 17, …. are prime numbers.
Composite Number: A Composite Number is a number which can be divided evenly. Any composite number has additional factors than 1 and itself.
For example: 4, 6, 8, 9, 10 …..
Co-primes or Relatively prime numbers: A pair of numbers not having any common factors other than 1 or –1. (Or alternatively their greatest common factor is 1 or –1)
For Example: 15 and 28 are co-prime, because the factors of 15 (1,3,5,15) , and the factors of 28 (1,2,4,7,14,28) are not in common (except for 1) .
Twin Primes: A pair of prime numbers that differ by 2 (successive odd numbers that are both Prime numbers) .
For Example: (3,5) , (5,7) , (11,13) .
Fractions
A fraction is known as a rational number and written in the form of p/q where p and q are integers and q ≠ 0. The lower number ‘q’ is known as denominator and the upper number ‘p’ is known as numerator.
Type of Fractions
Proper Fraction: The fraction in which numerator is less the denominator is called a proper fraction.
For Example: 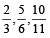 etc.
etc.
Improper fraction: The fraction in which numerator is greater than the denominator is called improper fraction.
For Example: 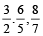 , etc
, etc
Mixed fraction: Mixed fraction is a composition of fraction and whole number.
For example: 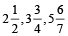 etc.
etc.
Complex fraction: A complex fraction is that fraction in which numerator or denominator or both are fractions.
For Example: 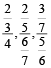 , etc.
, etc.
Decimal fraction: The fraction whose denominator is 10 or its higher power, is called a decimal fraction.
For Example: 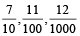
Continued fraction: Fractions which contain addition or subtraction of fractions or a series of fractions generally in denominator (sometimes in numerator also) are called continued fractions.
It is also defined as a fraction whose numerator is an integer and whose denominator is an integer plus a fraction.
For Example: 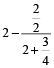
Comparison of Fractions
If the denominators of all the given fractions are equal then the fraction of greater numerator will be the greater fraction.
For Example: 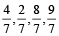 then,
then, 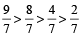
If the numerators of all the given fractions are equal then the fraction of smaller denominator will be greater fraction.
For Example: 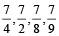 then,
then, 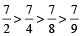
When numerator is greater than denominator and the differences of numerator and denominator are equal, then the fraction of smaller numerator will be the greater faction.
For Example: 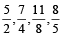 then,
then, 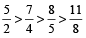
Quicker Method (Cross Multiplication)
This is a short-cut method to compare fractions. Using this method we can compare all types of fractions.
The fraction whose numerator is in the greater product is greater.
Since 36 is greater than 35, hence,
Divisibility Rules
- Divisibility by 2: A number is divisible by 2 if its unit’s digit is even or 0.
- Divisibility by 3: A number is divisible by 3 if the sum of its digits are divisible by 3.
- Divisibility by 4: A number is divisible by 4 if the last 2 digits are divisible by 4, or if the last two digits are 0’s.
- Divisibility by 5: A number is divisible by 5 if its unit’s digit is 5 or 0.
- Divisibility by 6: A number is divisible by 6 if it is simultaneously divisible by 2 and 3.
- Divisibility by 7: A number is divisible by 7 if unit’s place digit is multiplied by 2 and subtracted from the remaining digits and the number obtained is divisible by 7.
- Divisibility by 8: A number is divisible by 8 if the last 3 digits of the number are divisible by 8, or if the last three digits of a number are zeros.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
- Divisibility by 10: A number is divisible by 10 if its unit’s digit is 0.
- Divisibility by 11: A number is divisible by 11 if the sum of digits at odd and even places are equal or differ by a number divisible by 11.
- Divisibility by 12: A number is divisible by 12 if the number is divisible by both 4 and 3.
- Divisibility by 13: A number is divisible by 13 if its unit’s place digit is multiplied by 4 and added to the remaining digits and the number obtained is divisible by 13.
- Divisibility by 14: A number is divisible by 14 if the number is divisible by both 2 and 7.
- Divisibility by 15: A number is divisible by 15 if the number is divisible by both 3 and 5.
- Divisibility by 16: A number is divisible by 16 if its last 4 digits is divisible by 16 or if the last four digits are zeros.
- Divisibility by 17: A number is divisible by 17 if its unit’s place digit is multiplied by 5 and subtracted from the remaining digits and the number obtained is divisible by 17.
- Divisibility by 18: A number is divisible by 18 if the number is divisible by both 2 and 9.
- Divisibility by 19: A number is divisible by 19 if its unit’s place digit is multiplied by 2 and added to the remaining digits and the number obtained is divisible by 19.