Time limit: 0
Finish Test
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
- Most Important Multiple Choice Questions
- Online Geometry Exercise with Correct Answer Key and Solutions
- Useful for all Competitive Exams
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
- Question 1 of 20
1. Question
The sum of the interior angles of a polygon is 1620°. The number of sides of the polygon are
Hint
The sum of the interior angles of a polygon of n sides is given by the expression (2n – 4) π/2
⇒
⇒ 2n = 22
⇒ n = 11
Thus the no. of sides of the polygon are 11.
- Question 2 of 20
2. Question
A cyclic parallelogram having unequal adjacent sides is necessarily a :
Hint
It is a rectangle.
(In a cyclic parallelogram each angle is equal to 90°. So, it is definitely either a square or a rectangle. Since the given cyclic parallelogram has unequal adjacent sides, it is a square.)
- Question 3 of 20
3. Question
If the angles of a triangle are in the ratio 5 : 3 : 2, then the triangle could be :
Hint
Let the angles of the triangle be 5x, 3x and 2x.
Now, 5x + 3x + 2x = 180°
⇒ 10x = 180
⇒ x = 18
⇒ Angles are 36, 54 and 90°
Given ∆ is right angled.
- Question 4 of 20
4. Question
If one of the diagonals of a rhombus is equal to its side, then the diagonals of the rhombus are in the ratio:
Hint
Let the diagonals of the rhombus be x and y and the its sides be x
Now,
⇒
⇒ 3x² = y²
⇒
⇒ y : x
- Question 5 of 20
5. Question
In the given figure, ∠ ABC and ∠ DEF are two angles such that BA ⊥ ED and EF ⊥ BC, then find value of ∠ ABC + ∠ DEF.
Hint
Since the sum of all the angle of a quadrilateral is 360°
We have ∠ ABC + ∠ BQE + ∠ DEF + ∠ EPB = 360°
∴ ∠ ABC + ∠ DEF = 180°
[since BPE = EQB = 90° ]
- Question 6 of 20
6. Question
In the given figure given below, E is the mid-point of AB and F is the midpoint of AD. if the area of FAEC is 13, what is the area of ABCD?
Hint
As F is the mid-point of AD, CF is the median of the triangle ACD to the side AD.
Hence area of the triangle FCD = area of the triangle ACF.
Similarly area of triangle BCE = area of triangle ACE.
∴ Area of ABCD = Area of (CDF + CFA + ACE + BCE)
= 2 Area (CFA + ACE) = 2 × 13 = 26 sq. units.
- Question 7 of 20
7. Question
Give that segment AB and CD are parallel, if lines ℓ, m and n intersect at point O. Find the ratio of θ to ∠ODS
Hint
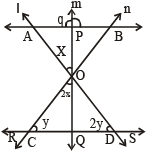
Let the line m cut AB and CD at point P and Q respectively
∠ DOQ = x (exterior angle)
Hence, Y + 2x (corresponding angle)
∴ y = x …(1)
Also . ∠ DOQ = x (vertically opposite angles)
In ∆ OCD, sum of the angles = 180⁰
∴ y + 2y + 2x + x =180°
⇒ 3x + 3y = 180°
⇒ x + y = 60 …(2)
From (1) and (2)
x = y = 30 = 2y = 60
∴ ∠ ODS = 180 – 60 = 120°
∴ θ = 180 – 3x = 180 – 3(30) = 180 – 90 = 90°.
∴ The required ratio = 90 : 120 = 3 : 4.
- Question 8 of 20
8. Question
AB ⊥ BC and BD ⊥ AC. CE bisects the angle C. ∠A = 30°. Then, what is ∠CED?
Hint
In ∆ ABC, = ∠C = 180 – 90 – 30 = 60°
Again in ∆ DEC, = ∠ CED = 180 – 90 – 30 = 60°
- Question 9 of 20
9. Question
In triangle ABC, angle B is a right angle. If (AC) is 6 cm, and D is the mid – point of side AC. The length of BD is
Hint
In a right angled ∆, the length of the median is ½ the length of the hypotenuse .
Hence BD = ½ AC = 3 cm
- Question 10 of 20
10. Question
ABCD is a square of area 4, which is divided into four non overlapping triangles as shown in the fig. Then the sum of the perimeters of the triangles is
Hint
ABCD is square a² = 4 ⇒ a = 2
perimeters of four triangles
= AB + BC + CD + DA + 2(AC + BD)
- Question 11 of 20
11. Question
The sides of a quadrilateral are extended to make the angles as shown below :
What is the value of x?Hint
Sum of all the interior angles of a polygon taken in order is 360°.
i.e., x + 90 + 115 + 75 = 360
⇒ x = 360° – 280° = 80°
⇒ x = 80°
- Question 12 of 20
12. Question
Instead of walking along two adjacent sides of a rectangular field, a boy took a short cut along the diagonal and saved a distance equal to half the longer side. Then the ratio of the shorter side to the longer side is
Hint
According to question,
- Question 13 of 20
13. Question
If two parallel lines are cut by two distinct transversals, then the quadrilateral formed by these four lines will always be a :
Hint
The quadrilateral obtained will always be a trapeziam as it has two lines which are always parallel to each other.
- Question 14 of 20
14. Question
In the following figure, find ∠ADC.
Hint
∠ACB = ∠BAC (Angles opposite equal sides are equal)
Similarly, ∠ADC = ∠CAD
∴ ∠ACB = ∠BAC
⇒ ∠ADC = ∠CAD
- Question 15 of 20
15. Question
In a triangle ABC, the internal bisector of the angle A meets BC at D. If AB = 4, AC = 3 and ∠A = 60°, then the length of AD is
Hint
Using the theorem of angle of bisector,
In ∆ABD, by sine rule,
…(1)In ∆ABC, by sine rule;
⇒
[putting the value of sin B from (1)]
- Question 16 of 20
16. Question
In the figure AG = 9, AB = 12, AH = 6, Find HC.
Hint
m ∠ AHG = 180 – 108 = 72⁰
∴ ∠ AHG = ∠ ABC …..(same angle with different names)
∴ ∆ AHG – ∆ABC …..(AA test for similarity)
AH/AB = AG/AG;
⇒ 6/12 = 9/AC
∴ AC =
= 18∴ HC = AC – AH = 18 – 6 = 12
- Question 17 of 20
17. Question
In ∆ABC, DE || BC and AD/DB = 3/5. If AC = 5.6 cm, find AE.
Hint
In ∆ABC, DE || BC
By applying basic Proportionality theorem,
But
∴
⇒
⇒
⇒
⇒ 8AE = 3 × 5.6
⇒ AE = 3 × 5.6/8
∴ AE = 2.1 cm.
- Question 18 of 20
18. Question
In the given fig. AB || QR, find the length of PB.
Hint
∆PAB ~ ∆PQR
∴ PB = 2cm
- Question 19 of 20
19. Question
In a triangle ABC, the lengths of the sides AB, AC and BC are 3, 5 and 6 cm, respectively. If a point D on BC is drawn such that the line AD bisects the angle A internally, then what is the length of BD?
Hint
As AD bisects ∠BAC, we have
⇒
⇒
⇒
⇒
⇒
= 2.25 cm
- Question 20 of 20
20. Question
The number of tangents that can be drawn to two non-intersecting circles is :
Hint
Four tangents can be drawn to two non-intersecting circles in the following manner :
