Probability Exercise 1

If the drawn ball is neither red nor green, then it must be blue, which can be picked in ⁷C₁ = 7 ways. One ball can be picked from the total (8 + 7 + 6 = 21) in ²¹C₁ = 21 ways.

∴ Required probability

There are 5 + 7 = 12 balls in the bag and out of these two balls can be drawn in ¹²C₂ ways. There are 5 green balls, therefore, one green ball can be drawn in ⁵C₁ ways; similarly, one red ball can be drawn in ⁷C₁ ways so that the number of ways in which we can draw one green ball and the other red is ⁵C₁ × ⁷C₁.

Hence, P (one green and the other red)

There are 7 + 5 = 12 balls in the bag and the number of ways in which 4 balls can be drawn is ¹²C₄ and the number of ways of drawing 4 black balls (out of seven) is ⁷C₄.

Hence, P (4 black balls)

Thus the odds against the event ‘all black balls’ are

Total number of balls = 12

Hence, required probability

No of ways of drawing 2 white balls from 5 white balls = ⁵C₂.

Also, No of ways of drawing 2 other from remaining 7 balls = ⁷C₂

Since each ball can be put into any one of the three boxes. So, the total number of ways in which 12 balls can be put into three boxes is 3¹².
Out of 12 balls, 3 balls can be chosen in ¹²C₃ ways. Now, remaining 9 balls can be put in the remaining 2 boxes in 2⁹ ways. So, the total number or ways in which 3 balls are put in the first box and the remaining in other two boxes is ¹²C₃ × 2⁹.
Hence, required probability

2 balls can be drawn in the following ways

1 red and 1 green or 2 red or 2 green

Required probability

=

and

⇒ p₁ > p₂

n(S) =

No. of selection of 3 oranges out of the total 12 oranges

= ¹²C₃ = 2 × 11 × 10 = 220.

No. of selection of 3 bad oranges out of the total 4 bad oranges = ⁴c₃ = 4

∴ n(E) = no. of desired selection of oranges

= 220 – 4 = 216

∴ P (E) =

Total no. of ways of drawing 3 marbles

Total no. of ways of drawing marbles, which are of same colour

= ⁵C₃ + ⁴C₃ + ³C₃

= 10 + 4 + 1 = 15

∴ Probability of same colour

= = ³⁄₄₄

∴ Probability of not same colour

= 1 – ³⁄₄₄ = ⁴¹⁄₄₄

When two are thrown then there are 6 × 6 exhaustive cases

∴ n = 36. Let A denote the event “total score of 7” when 2 dice are thrown then A

= [(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)].

Thus there are 6 favourable cases.

∴ m = 6

By definition

Let W stand for the winning of a game and L for losing it. Then there are 4 mutually exclusive possibilities

(i) W, W, W
(ii) W, W, L, W
(iii) W, L, W, W
(iv) L, W, W, W.

[Note that case (i) includes both the cases whether he losses or wins the fourth game.]

By the given conditions of the question, the probabilities for (i), (ii), (iii) and (iv) respectively are

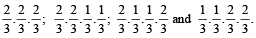
Hence the required probability

=

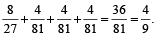
[Since the probability of winning the game if previous game was also won is 2/(1+2) = 2/3 and the probability of winning the game if previous game was a loss is 1/(1+2) = 1/3].

Probability that only husband is selected

Probability that only wife is selected

=

∴ Probability that only one of them is selected

Total of seven can be obtained in the following ways
1, 1, 1, 4 in = 4 ways [there are four objects, three repeated]
Similarly,
1, 1,2, 3 in = 12 ways
1, 2,2, 2 in = 4 ways
Hence, required probability

[Since exhaustive no. of cases = 6 × 6 × 6 × 6 = 6⁴]

The number of ways of getting the different number 1, 2, ....., 6 in six dice = 6!.

Total number of ways = 6⁶

Hence, required probability

=

The faulty machines can be identified in two tests only if both the tested machines are either all defective or all non-defective. See the following tree diagram.

(Here D is for Defective & ND is for Non Defective)

Required Probability

=

Since the probability that first machine is defective (or non-defective) is ²⁄₄ and the probability that second machine is also defective (or non - defective) is ⅓ as 1 defective machine remains in total three machines.

The probability that the person hits the target = 0.3

∴ The probability that he does not hit the target in a trial

= 1 – 0.3 = 0.7

∴ The probability that he does not hit the target in any of the ten trials = (0.7)¹⁰

∴ Probability that he hits the target

= Probability that at least one of the trials succeeds

= 1 – (0.7)¹⁰.

The probability that A cannot solve the problem

The probability that B cannot solve the problem

The probability that both A and B cannot solve the problem

∴ The probability that at least one of A and B can solve the problem

∴ The probability that the problem is solved = ¹¹⁄₁₂

Seven people can seat themselves at a round table in 6! ways. The number of ways in which two distinguished persons will be next to each other = 2 (5) !, Hence, the required probability

The condition implies that the last digit in both the integers should be 0, 1, 5 or 6 and the probability

[ Since the squares of numbers ending in 0 or 1 or 5 or 6 also 0 or 1 or 5 or 6 respectively]

Exhaustive number of cases = 12
Favourable cases = ¹²C₂ (2⁶ – 2)
∴ Probability