Time limit: 0
Finish Test
0 of 36 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
Information
- Most Important Multiple Choice Questions
- Online Mensuration Exercise with Correct Answer Key and Solutions
- Useful for all Competitive Exams
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 36 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- Answered
- Review
- Question 1 of 36
1. Question
The water from a roof, 9 sq metres in area, flows down to a cylinder container of 900 cm² base. To what height will the water rise in cylinder if there is a rainfall of 0.1 mm?
Hint
Let height will be h cm.
Volume of water in roof = Volume of water in cylinder
⇒
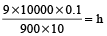
∴ h = 1 cm
- Question 2 of 36
2. Question
The trunk of a tree is a right cylinder 1.5 m in radius and 10 m high. The volume of the timber which remains when the trunk is trimmed just enough to reduce it to a rectangular parallelepiped on a square base is
Hint
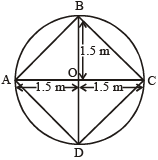
From ∆AOB,
AB =
=
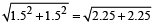
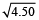
∴ Area of the square base of the trunk of the tree
=
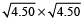
= 4.50 m²
∴ Volume of the timber = Area of base × height
= 4.50 × 10 = 45 m³
- Question 3 of 36
3. Question
The capacity of a cylindrical tank is 246.4 litres. If the height is 4 metres, what is the diameter of the base?
Hint
Volume of the tank
= 246.4 litres = 246400 cm³.
Let the radius of the base be r cm. Then,
∴ Diameter of the base
= 2r = 28 cm = .28 m
- Question 4 of 36
4. Question
A monument has 50 cylindrical pillars each of diameter 50 cm and height 4 m. What will be the labour charges for getting these pillars cleaned at the rate of 50 paise per sq. m? [use π = 3.14]
Hint
Curved surface area of cylinder = 2πrh
∴ Surface area of 50 cylindrical pillars
= 50 × 2πrh
Now, Diameter of each cylindrical pillar = 50 cm
∴ Radius = 50/2= 25 cm = 0.25 m
Also, height = 4m
∴ Surface area
= 50 × 2 × 3.14 ×. 25 × 4
= 314 × 1 sq m.
= 314 sq. m.
Now, labour charges at the rate of 50 paise
per sq. m = 314 ×.5 = 157.0
= Rs 157
- Question 5 of 36
5. Question
A cylindrical bucket of height 36 cm and radius 21 cm is filled with sand. The bucket is emptied on the ground and a conical heap of sand is formed, the height of the heap being 12 cm. The radius of the heap at the base is:
Hint
Volume of the bucket = volume of the sand emptied
Volume of sand = π (21)² × 36
Let r be the radius of the conical heap.
Then,
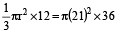
⇒ r² = (21)² × 9
⇒ r = 21 × 3 = 63
- Question 6 of 36
6. Question
A conical vessel, whose internal radius is 12 cm and height 50 cm, is full of liquid. The contents are emptied into a cylindrical vessel with internal radius 10 cm. Find the height to which the liquid rises in the cylindrical vessel.
Hint
Volume of the liquid in the cylindrical vessel
= Volume of the conical vessel
=
=
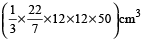
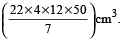
Let the height of the liquid in the vessel be h.
Then,
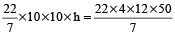
⇒ h =
- Question 7 of 36
7. Question
A right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and the height are in the ratio 5 : 12, then the ratio of the total surface area of the cylinder to that of the cone is
Hint
Let the radius of the base are 5k and 12k respectively
∴
=
=
+ 
=
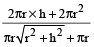
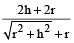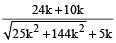
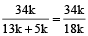= 17/9 - Question 8 of 36
8. Question
A cone of height 9 cm with diameter of its base 18 cm is carved out from a wooden solid sphere of radius 9 cm. The percentage of the wood wasted is:
Hint
Volume of sphere
=
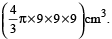
Volume of cone
=
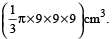
Volume of wood wasted
=
= (π × 9 × 9 × 9) cm³
∴ Required percentage
=
=
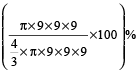
- Question 9 of 36
9. Question
A conical vessel of base radius 2 cm and height 3 cm is filled with kerosene. This liquid leaks through a hole in the bottom and collects in a cylindrical jar of radius 2 cm. The kerosene level in the jar is
Hint
Let the kerosene level of cylindrical jar be h.
Now, Volume of conical vessel
= ⅓ πr²h
Since, radius (r)
= 2 cm and height(h) = 3cm of conical vessel.
∴ Volume = ⅓ π × 4 × 3 = 4 π
Now, Volume of cylindrical jar = πr²h
= π (2)²h = 4πh
Now, Volume of conical vessel = Volume of cylindrical Jar
⇒ 4 π = 4 πh
⇒ h = 1cm
Hence, kerosene level in Jar is 1 cm.
- Question 10 of 36
10. Question
If the volume of a sphere is divided by its surface area, the result is 27 cms. The radius of the sphere is
Hint
In a sphere,
volume
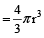
and surface area
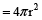
According to question,
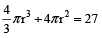
or r = 27 × 3 = 81 cm
- Question 11 of 36
11. Question
A cylinder is circumscribed about a hemisphere and a cone is inscribed in the cylinder so as to have its vertex at the centre of one end, and the other end as its base. The volume of the cylinder, hemisphere and the cone are, respectively in the ratio:
Hint
We have,
radius of the hemisphere = radius of the cone
= height of the cone
= height of the cylinder = r (say)
Then, ratio of the volumes of cylinder, hemisphere and cone
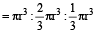
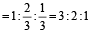
- Question 12 of 36
12. Question
A copper sphere of radius 3 cm is beaten and drawn into a wire of diameter 0.2 cm. The length of the wire is
Hint
Let the length of the wire be h cm.
and radius of sphere and wire are R and r respectively.
then, volume of sphere = volume of wire (cylinder)
⇒
⇒
⇒
∴
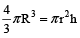
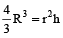
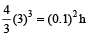
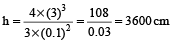= 36 m - Question 13 of 36
13. Question
A spherical ball of lead, 3 cm in diameter, is melted and recast into three spherical balls. The diameter of two of these balls are 1.5 cm and 2 cm respectively. The diameter of the third ball is
Hint
Let radius of the 3rd spherical ball be R,
∴
⇒
⇒
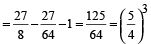
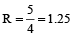
∴ Diameter of the third spherical ball
= 1.25 × 2 = 2.5 cm.
- Question 14 of 36
14. Question
If the radius of a sphere is increased by 2 cm, then its surface area increases by 352 cm². The radius of the sphere before the increase was:
Hint
4π (r + 2)² – 4πr² = 352
⇒ (r + 2)² – r²
=
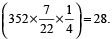
⇒ (r + 2 + r)(r + 2 – r) = 28
⇒ 2r + 2 = ²⁸⁄₂
⇒ 2r + 2 = 14 ⇒ r = 6 cm
- Question 15 of 36
15. Question
A rectangular tank measuring 5m × 4.5 m × 2.1 m is dug in the centre of the field measuring 13.5 m × 2.5. The earth dug out is spread evenly over the remaining portion of a field. How much is the level of the field raised?
Hint
Area of the field
= 13.5 × 2.5 = 33.75 m²
Area covered by the rectangular tank
= 5 × 4.5 = 22.50 m²
Area of the field on which the earth dug out is to be spread
= 33.75 – 22.50 = 11.25 m²
Let the required height be h.
Then, 11.25 × h = 5 × 4.5 × 2.1
⇒ h = 4.2 m
- Question 16 of 36
16. Question
A metal cube of edge 12 cm is melted and formed into three smaller cubes. If the edges of two smaller cubes are 6 cm and 8 cm, then find the edge of the third smaller cube.
Hint
Let the edge of the third cube be x cm.
Then, x³ + 6³ + 8³ = 12³
⇒ x³ + 216 + 512 = 1728
⇒ x³ = 1000
⇒ x = 10.
Thus the edge of third cube = 10 cm.
- Question 17 of 36
17. Question
The surface area of a cube is 150 m². The length of its diagonal is
Hint
In a cube, Area = 6 (side)²
⇒ 150 = 6 (side)²
∴ side =
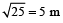
Length of diagonal
=
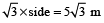
- Question 18 of 36
18. Question
The length of the longest rod that can be placed in a room which is 12 m long, 9 m broad and 8 m high is:
Hint
Required length = length of the diagonal
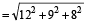
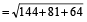
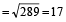m - Question 19 of 36
19. Question
The volume of water measured on a rectangular field 500 m × 300 m is 3000 m³. Find the depth (amount) of rain that has fallen.
Hint
Let depth of rain be h metre. Then,
volume of water = area of rectangular field × depth of rain
⇒ 3000 = 500 × 300 × h
∴
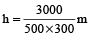
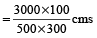
= 2 cms
- Question 20 of 36
20. Question
A cistern 6 m long and 4 m wide contains water up to a depth of 1 m 25 cm. The total area of the wet surface is:
Hint
Area of the wet surface
= [2(lb + bh + lh) – lb] = 2(bh + lh) + lb
= [2(4 × 1.25 + 6 × 1.25) +6 × 4] m² = 49 m².
- Question 21 of 36
21. Question
The internal measurements of a box with lid are 115 × 75 × 35 cm³ and the wood of which it is made is 2.5 cm thick. Find the volume of wood.
Hint
Internal volume
= 115 × 75 × 35 = 301875 cm³
External volume
= (115 + 2 × 2.5) × (75 + 2× 2.5)× (35+2×2.5)
= 120 × 80 × 40 = 3,84,000 cm³
∴ Volume of wood = External volume – Internal volume
= 3,84,000 – 3,01,875 = 82,125 cm³
- Question 22 of 36
22. Question
A rectangular tank is 225 m by 162 m at the base. With what speed must water flow into it through an aperture 60 cm by 45 cm that the level may be raised 20 cm in 5 hours?
Hint
Required speed of flow of water
=
=
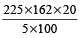
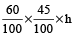
∴ h = 5400
- Question 23 of 36
23. Question
A cuboidal block of 6 cm × 9 cm × 12 cm is cut up into an exact number of equal cubes. The least possible number of cubes will be:
Hint
Volume of block
= (6 × 9 × 12) cm³
= 648 cm³.
Side of largest cube = H.C.F. of 6 cm, 9 cm, 12 cm = 3 cm.
Volume of the cube
= (3 × 3 × 3) = 27 cm³.
∴ Number of cubes
=
- Question 24 of 36
24. Question
A wooden box of dimensions 8m × 7m × 6m is to carry rectangular boxes of dimensions 8 cm × 7 cm × 6cm. The maximum number of boxes that can be carried in the wooden box is
Hint
Dimensions of wooden box
= 8m × 7m × 6m
= 800 cm × 700 cm × 600 cm
and dimensions of rectangular
boxes = 8 cm × 7 cm × 6 cm
∴ No. of boxes
=
=
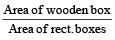
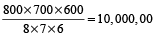
- Question 25 of 36
25. Question
The ratio of height of a room to its semi-perimeter is 2 : 5. It costs Rs 260 to paper the walls of the room with paper 50 cm wide at Rs 2 per metre allowing an area of 15 sq. m for doors and windows. The height of the room is:
Hint
Let h = 2x metres and (ℓ + b) = 5x metres.
Length of the paper
=
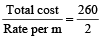m = 130 m.Area of the paper
=
Total area of 4 walls
= (65 + 15) m² = 80 m².
∴ 2(ℓ + b) × h = 80
⇒ 2 × 5x × 2x = 80
⇒ x² = 4
⇒ x = 2.
∴ Height of the room = 4 m.
- Question 26 of 36
26. Question
The length, breadth and height of a cuboid are in the ratio 1 : 2 : 3. The length, breadth and height of the cuboid are increased by 100%, 200% and 200%, respectively. Then, the increase in the volume of the cuboid will be:
Hint
Let the length, breadth and height of the cuboid be x, 2x and 3x, respectively.
Therefore, volume = x × 2x × 3x = 6x³
New length, breadth and height
= 2x, 6x and 9x, respectively.
New volume = 108x³
Thus, increase in volume
= (108 – 6)x³ = 102 x³
- Question 27 of 36
27. Question
Water flows into a tank 200 m × 150 m through a rectangular pipe 1.5 m × 1.25 m @ 20 kmph. In what time (in minutes) will the water rise by 2 metres?
Hint
Volume required in the tank
= (200 × 150 × 2) m³
= 60000 m³.
Length of water column flown in 1 min.
=
Volume flown per minute
=
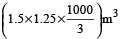
= 625 m³.
∴ Required time
=
- Question 28 of 36
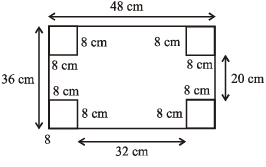
28. Question
A metallic sheets is of rectangular shape with dimensions 48 cm × 36 cm. From each one of its corners, a square of 8 cm is cut off. An open box is made of the remaining sheet. Find the volume of the box
Hint
Volume of the box made of the remaining sheet
= 32 × 20 × 8 = 5120 cm³
- Question 29 of 36
29. Question
A cube of 384 cm² surface area is melt to make x number of small cubes each of 96 mm² surface area. The value of x is
Hint
Let ‘A’ be the side of bigger cube and ‘a’ be the side of smaller cube
Surface area of bigger cube = 6 A²
⇒ 384 = 6A²
∴ A = 8 cm.
Surface area of smaller cube = 6a²
96 = 6a²
∴ a = 4 mm = 0.4 cm
So, Number of small cube
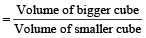
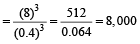
- Question 30 of 36
30. Question
It is required to fix a pipe such that water flowing through it at a speed of 7 metres per minute fills a tank of capacity 440 cubic metres in 10 minutes. The inner radius of the pipe should be:
Hint
Let inner radius of the pipe be r. Then,
⇒
⇒
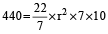
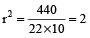
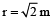
- Question 31 of 36
31. Question
A cylinder is filled to 4/5th its volume. It is then filled so that the level of water coincides with one edge of its bottom and top edge of the opposite side, In the process, 30 cc of the water is spilled. What is the volume of the cylinder?
Hint
Let the original volume of cylinder be V .
When it is filled ⅘, then it’s volume = ⅘V
When cylinder is filled, the level of water coincides with opposite sides of bottom and top edges then
Volume become = ½V
Since, in this process 30 cc of the water is spilled, therefore
⇒
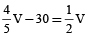
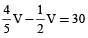
⇒ V (3/10) = 30
⇒ V = 100 cc
- Question 32 of 36
32. Question
A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is four times the radius of its base, then find the radius of the ice-cream cone.
Hint
Volume of the cylinder container
= π × 6² × 15 cu. cm …(1)
Let the radius of the base of the cone be r cm,
then, height of the cone = 4r cm
∴ Volume of the 10 cylindrical cones of ice-cream with hemispherical tops
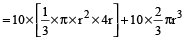
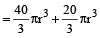
= 20 πr³ cu. cm …(2)
Since the whole ice-cream in the cylindrical container is distributed among 10 children in cones with hemispherical tops,
∴ (1) and (2), gives
⇒ π × 6² × 15 = 20πr³
⇒ r³ =
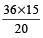= 27⇒ r = 3 cm
- Question 33 of 36
33. Question
A hemispherical bowl is filled to the brim with a beverage. The contents of the bowl are transfered into a cylindrical vessel whose radius is 50% more than its height. If the diameter is same for both the bowl and the cylinder, the volume of the beverage in the cylindrical vessel is: (i.e., some liquid will be left in the bowl.)
Hint
Let the height of the vessel be x.
Then, radius of the bowl
= radius of the vessel = x/2.
Volume of the bowl,
Volume of the vessel,
Since V₂ > V₁, so the vessel can contain 100% of the beverage filled in the bowl.
- Question 34 of 36
34. Question
An ice-cream company makes a popular brand of ice-cream in rectangular shaped bar 6 cm long, 5 cm wide and 2 cm thick. To cut the cost, the company has decided to reduce the volume of the bar by 20%, the thickness remaining the same, but the length and width will be decreased by the same percentage amount. The new length L will satisfy:
Hint
L × B × 2 = 48
⇒ L × B = 24
Now, 6 – 6 × 10% = 5.4,
5 – 5 × 10% = 4.5 and
Therefore, 5.4 × 4.5 = 24.3
Clearly, 5 < L < 5.5
- Question 35 of 36
35. Question
If the radius of a circle is diminished by 10%, the area is diminished by
Hint
If the radius is diminished by r%, then
Area is diminished by
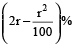
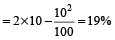
- Question 36 of 36
36. Question
The length of a rectangular plot is increased by 25%. To keep its area unchanged, the width of the plot should be:
Hint
Let the original length and breadth be both 10 cm each.
Then original area = 100 cm²
New length = 10 × 1.25 = 12.5 cm
Let new breadth be x. Then, 12.5x = 100
⇒
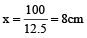
Hence, % reduction in breadth
=
