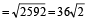Time limit: 0
Finish Test
0 of 27 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
Information
- Most Important Multiple Choice Questions
- Online Mensuration Exercise with Correct Answer Key and Solutions
- Useful for all Competitive Exams
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 27 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- Answered
- Review
- Question 1 of 27
1. Question
In an isoscele right angled triangle, the perimeter is 20 metre. Find its area.
Hint
In an isoscele right angled triangle,
Area = 1/23.3 × perimeter²
= 1/23.3 × 20² = 17.167 m²
- Question 2 of 27
2. Question
The area of a triangle is 615 m². If one of its sides is 123 metre, find the length of the perpendicular dropped on that side from opposite vertex.
Hint
In a triangle,
Area
⇒
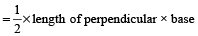
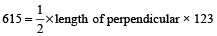
∴ Length of perpendicular
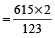= 10 m. - Question 3 of 27
3. Question
The altitude drawn to the base of an isosceles triangle is 8 cm and the perimeter is 32 cm. The area of the triangle is
Hint
Let ABC be the isosceles triangle and AD be the altitude.
Let AB = AC = x.
Then, BC = (32 – 2x).
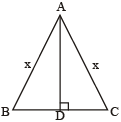
Since, in an isosceles triangle, the altitude bisects the base. So,
BD = DC = (16 – x).
In ∆ADC, AC² = AD² + DC²
⇒ x² = (8)² + (16 – x)²
⇒ 32x = 320
⇒ x = 10.
∴ BC = (32 – 2x)
= (32 – 20) cm
= 12 cm.
Hence, required area
=
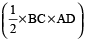
- Question 4 of 27
4. Question
In a triangle ABC, points P, Q and R are the mid-points of the sides AB, BC and CA respectively. If the area of the triangle ABC is 20 sq. units, find the area of the triangle PQR
Hint
Consider for an equilateral triangle. Hence ∆ABC consists of 4 such triangles with end points on mid points AB, BC and CA
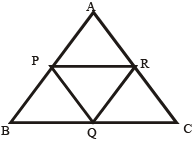
⇒ ¼ ar (∆ABC) = ar (∆PQR)
⇒ ar (∆PQR) = 5 sq. units
- Question 5 of 27
5. Question
How many squares are there in a 5 inch by 5 inch square grid, if the grid is made up one inch by one inch squares?
Hint
Required number of squares 5²/1² = 25
- Question 6 of 27
6. Question
If the ratio of areas of two squares is 9 : 1, the ratio of their perimeter is:
Hint
Let the area of two squares be 9x and x respectively.
So, sides of both squares will be
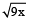and 
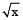respectively. [since, side = 
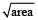]Now, perimeters of both squares will be
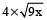and 
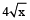respectively. [since, perimeter = 4 × side]Thus, ratio of their perimeters
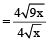= 3 : 1 - Question 7 of 27
7. Question
The area of a square field is 576 km². How long will it take for a horse to run around at the speed of 12 km/h?
Hint
Area of field = 576 km². Then,
each side of field
=
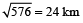
Distance covered by the horse Perimeter of square field
= 24 × 4 = 96 km
∴
= 96/12= 8 h
- Question 8 of 27
8. Question
A rectangular parking space is marked out by painting three of its sides. If the length of the unpainted side is 9 feet, and the sum of the lengths of the painted sides is 37 feet, then what is the area of the parking space in square feet?
Hint
Clearly, we have:
ℓ = 9 and ℓ + 2b
= 37 or b = 14.
∴ Area = (ℓ × b)
= (9 × 14) sq. ft.
= 126 sq. ft.
- Question 9 of 27
9. Question
A farmer wishes to start a 100 square metres rectangular vegetable garden. Since he has only 30 m barbed wire, he fences three sides of the garden letting his house compound wall act as the fourth side fencing. The dimension of the garden is:
Hint
We have : 2b + ℓ = 30
⇒ ℓ = 30 – 2b.
Area = 100 m²
⇒ ℓ × b = 100
⇒ b(30 – 2b) = 100
⇒ b² – 15b + 50 = 0
⇒ (b – 10) (b – 5) = 0
⇒ b = 10 or b = 5.
When b = 10, ℓ = 10 and when b = 5, ℓ = 20.
Since the garden is rectangular,
so its dimension is 20 m × 5 m.
- Question 10 of 27
10. Question
A rectangular plot 15 m ×10 m, has a path of grass outside it. If the area of grassy pathway is 54 m², find the width of the path.
Hint
Let the width of the path = W m
then, length of plot with path
= (15 + 2w) m
and breadth of plot with path
= (10 + 2 W) m
Therefore, Area of rectangular plot (without path)
= 15 × 10 = 150 m²
and Area of rectangular plot (with path)
= 150 + 54 = 204 m²
Hence, (15 + 2w) × (10 + 2w) = 204
⇒ 4w² + 50 w – 54 = 0
⇒ 2w² + 25 w – 27 = 0
⇒ (w – 2) (w + 27) = 0
Thus w = 2 or –27
∴ with of the path = 2 m
- Question 11 of 27
11. Question
The area of a rectangular field is 144 m². If the length had been 6 metres more, the area would have been 54 m² more. The original length of the field is
Hint
Let the length and breadth of the original rectangular field be x m and y m respectively.
Area of the original field
= x × y = 144 m²
∴
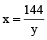… (i)If the length had been 6 m more, then area will be
(x + 6) y = 144 + 54
⇒ (x + 6) y = 198 … (ii)
Putting the value of x from eq (i) in eq (ii), we get
⇒ 144 + 6y = 198
⇒ 6y = 54 ⇒ y = 9 m
Putting the value of y in eq (i) we get x = 16 m
- Question 12 of 27
12. Question
The length and breadth of a playground are 36 m and 21 m respectively. Poles are required to be fixed all along the boundary at a distance 3 m apart. The number of poles required will be
Hint
Given, playground is rectangular.
Length = 36 m, Breadth = 21 m
Now, perimeter of playground
= 2( 21 + 36) = 114
Now, poles are fixed along the boundary at a distance 3m.
∴ Required no. of poles = ¹¹⁴⁄₃ = 38
- Question 13 of 27
13. Question
The cost of carpeting a room 18 m long with a carpet 75 cm wide at Rs 4.50 per metre is Rs 810. The breadth of the room is:
Hint
Length of the carpet
=
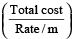
Area of the room = Area of the carpet
=
∴ Breadth of the room
=
= 7.5 m.
- Question 14 of 27
14. Question
If the perimeter and diagonal of a rectangle are 14 and 5 cms respectively, find its area.
Hint
In a rectangle,
⇒
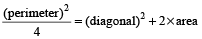
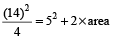
49 = 25 + 2 × area
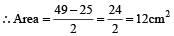
- Question 15 of 27
15. Question
A square carpet with an area 169 m² must have 2 metres cut-off one of its edges in order to be a perfect fit for a rectangular room. What is the area of rectangular room?
Hint
Side of square carpet
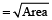
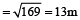
After cutting of one side,
Measure of one side
= 13 – 2 = 11 m
and other side = 13 m (remain same)
∴ Area of rectangular room
= 13 × 11 = 143 m²
- Question 16 of 27
16. Question
A picture 30 inch × 20 inch has a frame 2½ inch wide. The area of the picture is approximately how many times the area of the frame?
Hint
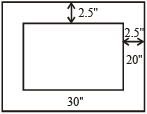
Length of frame
= 30 + 2.5 × 2 = 35 inch
Breadth of frame
= 20 + 2.5 × 2 = 25 inch
Now, area of picture
= 30 × 20 = 600 sq. inch
Area of frame
= (35 × 2.5) + (25 × 2.5) = 150
- Question 17 of 27
17. Question
The floor of a rectangular room is 15 m long and 12 m wide. The room is surrounded by a verandah of width 2 m on all its sides. The area of the verandah is:
Hint
Area of the outer rectangle = 19 × 16 = 304 m²
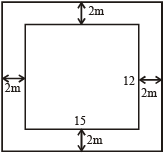
Area of the inner rectangle
= 15 × 12 = 180 m²
Required area
= (304 – 180) = 124 m²
- Question 18 of 27
18. Question
A typist uses a paper 12 inch by 5 inch length wise and leaves a margin of 1 inch at the top and the bottom and a margin of ½ inch on either side. What fractional part of the paper is available to him for typing?
Hint
Area of paper
= 12 × 5 = 60 sq. inch
Area of typing part
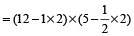
= (12 – 2) × (5 – 1)
= (10 × 4) sq. inch
∴ Required fraction
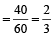
- Question 19 of 27
19. Question
A rectangular lawn 70 m × 30 m has two roads each 5 metres wide, running in the middle of it, one parallel to the length and the other parallel to the breadth. Find the cost of gravelling the road at the rate of Rs 4 per square metre.
Hint
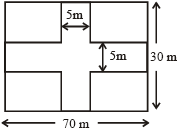
Total area of road
= Area of road which parallel to length + Area of road which parallel to breadth – overlapped road
= 70 × 5 + 30 × 5 – 5 × 5
= 350 + 150 – 25
= 500 – 25 = 475 m²
∴ Cost of gravelling the road
= 475 × 4 = Rs 1900
- Question 20 of 27
20. Question
The length and breadth of the floor of the room are 20 feet and 10 feet respectively. Square tiles of 2 feet length of different colours are to be laid on the floor. Black tiles are laid in the first row on all sides. If white tiles are laid in the one-third of the remaining and blue tiles in the rest, how many blue tiles will be there?
Hint
Area left after laying black tiles
= [(20 – 4) × (10 – 4)] sq. ft.
= 96 sq. ft.
Area under white tiles
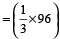sq. ft= 32 sq. ft.
Area under blue tiles
= (96 – 32) sq. ft = 64 sq. ft.
Number of blue tiles
=
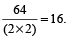
- Question 21 of 27
21. Question
The ratio between the length and the breadth of a rectangular park is 3 : 2. If a man cycling along the boundary of the park at the speed of 12km / hr completes one round in 8 minutes, then the area of the park (in sq. m) is:
Hint
Perimeter = Distance covered in 8 min.
Let length = 3x metres and breadth = 2x metres.
Then, 2 (3x + 2x) = 1600 or x = 160.
∴ Length = 480 m and Breadth = 320 m.
∴ Area = (480 × 320) m² = 153600 m².
- Question 22 of 27
22. Question
In measuring the side of a square, an error of 5% in excess is made. The error % in the calculated area is:
Hint
ℓ × b = 100 m²
⇒
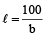
Therefore,
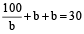
⇒ b² – 15b + 50 = 0
⇒ b = 10, 5
If we take b = 10, then garden becomes a square
Therefore, b = 5 m.
- Question 23 of 27
23. Question
The length of a room is double its breadth. The cost of colouring the ceiling at Rs 25 per sq. m is Rs 5,000 and the cost of painting the four walls at Rs 240 per sq. m is Rs 64,800. Find the height of the room.
Hint
Let the length of the room be ℓ m
Then its, breadth = ℓ/2
Therefore,
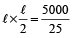
⇒ ℓ² = 400
⇒ ℓ = 20 m
Also,
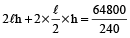
⇒ 3ℓh = 270
⇒
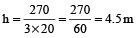
- Question 24 of 27
24. Question
A rectangular plate is of 6 m breadth and 12 m length. Two apertures of 2 m diameter each and one apertures of 1 m diameter have been made with the help of a gas cutter. What is the area of the remaining portion of the plate?
Hint
Given, Length = 12 m and Breadth = 6 m
∴ Area of rectangular plate
= 12 × 6 = 72 m²
Since, two apertures of 3 m diameter each have been made from this plate.
∴ Area of these two apertures
= π(1)² + π(1)²
= π + π = 2 π
Area of 1 aperture of 1m diameter
=
∴ Total area of aperture
=
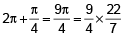= ⁹⁹⁄₁₄∴ Area of the remaining portion of the plate
= 72 – ⁹⁹⁄₁₄ sq. m
= ⁹⁰⁹⁄₁₄ sq. m ≈ 64.5 sq.m
- Question 25 of 27
25. Question
Four sheets 50 cm × 5 cm are arranged without overlapping to form a square having side 55 cm. What is the area of inner square so formed?
Hint
Side of the inner square
= 55 – 10 = 45
∴ Area of inner square
= 45 × 45 = 2025 sq. m.
- Question 26 of 27
26. Question
In the adjoining figure, AC + AB = 5 AD and AC – AD = 8. Then the area of the rectangle ABCD is
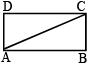
Hint
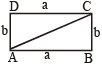
AC + AB = 5AD
⇒ AC + a = 5b …(1)
AC – AD = 8
⇒ AC = b + 8 …(2)
Using (1) and (2) ,
a + b + 8 = 5b
⇒ a + 8 = 4b …(3)
Using Pythagorous theorem,
a² + b² = (b + 8)² = b² + 64 + 16b
⇒ a² = 16b + 64 = (4b – 8)² = 16b² + 64 – 64b
⇒ 16b² – 80b = 0
⇒ b = 0 or 5
Putting b = 5 in (3),
a = 4b – 8 = 20 – 8 = 12
Area of rectangle = 12 × 5 = 60
- Question 27 of 27
27. Question
ABCD is a square, F is the mid-point of AB and E is a point on BC such that BE is one-third of BC. If area of ∆FBE = 108 m², then the length of AC is:
Hint
Let the side of the square be x, then,
BE = x/3 and BF = x/2
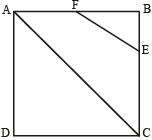
Area of ∆FEB
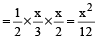
Now,
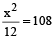
⇒ x² = 108 × 12 = 1296
In ∆ADC, we have
AC² = AD² + DC²
= x² + x² = 2x²
= 2 × 1296 = 2592
⇒ AC
