Permutation-Combination Exercise 3
You are here: Home1 / Maths2 / Permutation and Combination Exercise3 / Permutation-Combination Exercise 3
Time limit: 0
Finish Test
0 of 20 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
- Most Important Multiple Choice Questions
- Online Permutation and Combination Exercise with Correct Answer Key and Solutions
- Useful for all Competitive Exams
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 20 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Answered
- Review
- Question 1 of 20
1. Question
In a polygon no three diagonals are concurrent. If the total number of points of intersection of diagonals interior to the polygon be 70 then the number of diagonals of the polygon is
Hint
A combination of four vertices is equivalent to one interior point of intersection of diagonals.

∴ No. of interior points of intersection = nC₄ = 70
⇒ n (n – 1) (n – 2) (n – 3)
= 5. 6. 7. 8
∴ n = 8 So, number of diagonals
= ⁸C₂ – 8 = 20
- Question 2 of 20
2. Question
In how many ways can the eight directors, the Vice-chairman and the Chairman of a firm be seated at a round-table, if the Chairman has to sit between the Vice-chairman and the Director?
Hint
Let the Vice-chairman & the Chairman form 1 unit.
Along with the eight directors, we now have to arrange 9 different units in a circle.
This can be done in 8! ways.
At the some time, the Vice-chairman & the chairman can be arranged in two different ways.
Therefore, the total number of ways = 2 × 8!
- Question 3 of 20
3. Question
Out of 2n+1 students, n students have to be given the scholarships. The number of ways in which at least one student can be given the scholarship is 63. What is the number of students receiving the scholarship?
Hint
The no. of ways are
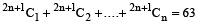
By option elimination,
2n + 1 = 7. So n = 3.
- Question 4 of 20
4. Question
How many three digit positive integers, with digits x, y and z in the hundred’s, ten’s and unit’s place respectively, exist such that x < y, z < y and x ≠ 0?
Hint
Consider the number:
x y z where x < y , z < y and x ≠ 0.
If y = 9 , x can be between 1 to 8 and z can be between 0 to 8
Total combinations = 9 × 8 = 72
If y = 8 , x can be between 1 to 7 and z can be between 0 to 7
combinations = 7 × 8 = 56
Similarly we add all combinations :
8 × 9 + 7 × 8 + 6 × 7 + 5 × 6 + 4 × 5 + 3 × 4 + 2 × 3 + 2 × 1
= 240 ways.
- Question 5 of 20
5. Question
There are 6 boxes numbered 1,2,………6. Each box is to be filled up either with a red or a green ball in such a way that at least 1 box contains a green ball and the boxes containing green balls are consecutively numbered. The total number of ways in which this can be done is
Hint
As they are consecutively numbered total number of ways will be
6 + 5 + 4 + 3 + 2 + 1 = 21 ways
- Question 6 of 20
6. Question
In a chess competition involving some boys and girls of a school, every student had to play exactly one game with every other student. It was found that in 45 games both the players were girls and in 190 games both were boys. The number of games in which one player was a boy and the other was a girl is
Hint
Let number of girls = x and the number of boys = y
45 games in which both the players were girls
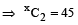
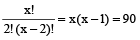
∴ x = 10
190 games, where both the players were boys.
yC₂ = 190
⇒ y(y – 1) = 380
∴ y = 20
Hence the total number of games in which one player was a boy and the other was a girl
= 10 × 20 = 200
- Question 7 of 20
7. Question
Three Englishmen and three Frenchmen work for the same company. Each of them knows a secret not known to others. They need to exchange these secrets over person-to-person phone calls so that eventually each person knows all six secrets. None of the Frenchmen knows English, and only one Englishman knows French. What is the minimum number of phone calls needed for the above purpose?
Hint
For each person to know all the secrets the communication has to be between the Englishmen (who knows say E1 French) and one Frenchmen (say F1).
The other two in each case will communicate with E1 & F1 respectively.
So for minimum no. of calls, E2 gives information to E1 & receives it after E1 interacts with F1.
So 2 calls for each of the four E2, E3, F2 and F3,
i.e., 8 calls +1 call (between E1 & F1). Hence 9 calls in all.
- Question 8 of 20
8. Question
A lady gives a dinner party to 5 guests to be selected from nine friends. The number of ways of forming the party of 5, given that two of the friends will not attend the party together is
Hint
Number of ways of selecting 5 guests from nine friends = ⁹C₅
Out of these, ⁷C₃ ways are those in which two of the friends occur together [3 more persons to be selected out of remaining 7]
∴ Number of ways, in which two of the friends will not attend the party together
= ⁹C₅ – ⁷C₃ = 91.
- Question 9 of 20
9. Question
In a chess tournament, where the participants were to play one game with another, two chess players fell ill, having played 3 games each. If the total number of games played is 84, the number of participants at the beginning was
Hint
Let there be n participants in the beginning.
Then the number of games played by (n – 2) players
= n – ²C₂
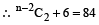
(Two players played three games each)
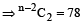
⇒ (n – 2)(n – 3) = 156
⇒ n² – 5n – 150 = 0
⇒ n = 15
- Question 10 of 20
10. Question
There are 10 bags B₁, B₂, B₃, …., B₁₀, which contain 21, 22, …., 30 different articles respectively. The total number of ways to bring out 10 articles from a bag is
Hint
The required number of ways
=
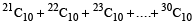
=
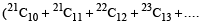
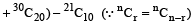
=
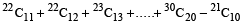
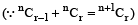
…………. =
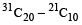 .
. - Question 11 of 20
11. Question
The number of ways in which a mixed doubles game in tennis can be arranged from 5 married couples, if no husband and wife play in the same game, is
Hint
Let the sides of the game be A and B. Given 5 married couples, i.e., 5 husbands and 5 wives.
Now, 2 husbands for two sides A and B can be selected out of 5 = ⁵C₂ = 10 ways.
After choosing the two husbands their wives are to be excluded (since no husband and wife play in the same game).
So we are to choose 2 wives out of remaining 5 – 2 = 3 wives
i.e., ³C₂ = 3 ways.
Again two wives can interchange their sides A and B in 2! = 2 ways.
By the principle of multiplication, the required number of ways
= 10 × 3 × 2 = 60
- Question 12 of 20
12. Question
Six teachers and six students have to sit round a circular table such that there is a teacher between any two students. The number of ways in which they can sit is
Hint

Six students S₁, S₂, …….., S₆ can be arranged round a circular table in 5 ! ways.
Among these 6 students there are six vacant places, shown by dots (•) in which six teachers can sit in 6 ! ways.
Hence, number of arrangement = 5 ! × 6 !
- Question 13 of 20
13. Question
m distinct animals of a circus have to be placed in m cages, one in each cage. If n (< m) cages are too small to accommodate p (n < p < m) animals, then the number of ways of putting the animals into cages are
Hint
Number of ways of arranging P big animals into
m – n big cages = m–nPp.
Now remaining animals can be arranged in any cage in
m–pPm–P ways
∴ Desired number of ways
= m–nPp × m–pPm–p
- Question 14 of 20
14. Question
A boy has 3 library cards and 8 books of his interest in the library. Of these 8, he does not want to borrow chemistry part II unless Chemistry part I is also borrowed. In how many ways can he choose the three books to be borrowed?
Hint
Two possibilities are there :
(i) Chemistry part I is available in 8 books with Chemistry part II.
or
(ii) Chemistry part II is available in 8 books but Chemistry part I is not available.
Total No. of ways
= 1 × ⁶C₁ + ⁷C₃
=
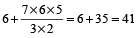
- Question 15 of 20
15. Question
There are 6 equally spaced points A, B, C, D, E and F marked on a circle with radius R. How many convex pentagons of distinctly different areas can be drawn using these points as vertices?
Hint
As all the points are equally spaced, the area of all the convex pentagons will be the same.
- Question 16 of 20
16. Question
Ten different letters of an alphabet are given. Words with 5 letters are formed from these given letters. Then the number of words which have at least one letter repeated is :
Hint
No. of words which have at least one letter repeated = total no. of words – total no. of words in which no letter is repeated
= 10⁵ – ¹⁰P₅
= 100000 – 10 × 9 × 8 × 7 × 6
= 100000 – 30240 = 69760
- Question 17 of 20
17. Question
In an examination paper there are two sections each containing 4 questions. A candidate is required to attempt 5 questions but not more than 3 questions from any particular section. In how many ways can 5 questions be selected?
Hint
Under the given restrictions, 5 questions can be selected in the following ways :
2 questions from the first section and 3 questions from the second section
Or
3 questions from the first section and 2 questions from the second section.
Required no. of ways
= ⁴C₂ × ⁴C₃ + ⁴C₃ × ⁴C₂
= 24 + 24 = 48
- Question 18 of 20
18. Question
A box contains 10 balls out of which 3 are red and the rest are blue. In how many ways can a random sample of 6 balls be drawn from the bag so that at the most 2 red balls are included in the sample and no sample has all the 6 balls of the same colour?
Hint
Six balls can be selected in the following ways: one red balls and 5 blue balls or
Two red balls and 4 blue balls
Total number of ways
= ³C₁ × ⁷C₅ + ³C₂ × ⁷C₄
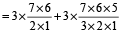
= 63 + 105 = 168
- Question 19 of 20
19. Question
A class photograph has to be taken. The front row consists of 6 girls who are sitting. 20 boys are standing behind. The two corner positions are reserved for the 2 tallest boys. In how many ways can the students be arranged?
Hint
Two tallest boys can be arranged in 2! ways. Rest 18 can be arranged in 18! ways.
Girls can be arranged in 6! ways.
Total number of ways of arrangement
= 2! × 18! × 6!
= 18! × 2 × 720 = 18! × 1440
- Question 20 of 20
20. Question
A,B,C and D are four towns any three of which are non-collinear. Then the number of ways to construct three roads each joining a pair of towns so that the roads do not form a triangle is
Hint
To construct 2 roads, three towns can be selected out of 4 in 4 ×3×2 = 24 ways.
Now if the third road goes from the third town to the first town, a triangle is formed, and if it goes to the fourth town, a triangle is not formed. So there are 24 ways to form a triangle and 24 ways of avoiding a triangle.
