Time limit: 0
Finish Test
0 of 27 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
Information
- Most Important Multiple Choice Questions
- Online Number System Exercise with Correct Answer Key and Solutions
- Useful for all Competitive Exams
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 27 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- Answered
- Review
-
Question 1 of 27
1. Question
If (74)² is subtracted from the square of a number, the answer so obtained is 5340. What is the number?
Hint
Let the number be x.
Then, x² – (74)² = 5340
⇒ x² = 5340 + 5476 = 10816
⇒ x =
-
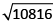
Question 2 of 27
2. Question
If (74)² is subtracted from the square of a number, the answer so obtained is 3740. What is the number?
Hint
Let the number be = x
According to the question
x² – (74)² = 3740
⇒ x² = 3740 + 5476 = 9216
∴ x =
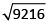= 96 -
Question 3 of 27
3. Question
If (46)² is subtracted from the square of a number, the answer so obtained is 485. What is the number?
Hint
Let the number be x
∴ x² – (46)² = 485
⇒ x² = 485 + (46)² = 2601
∴ x =
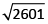= 51 -
Question 4 of 27
4. Question
If (57)² is added to the square of a number, the answer so obtained is 8010. What is the number?
Hint
Let the number be = x
According to the question,
x² + 57² = 8010
⇒ x² + 3249 = 8010
⇒ x² = 8010 – 3249 = 4761
⇒ x =
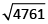= 69 -
Question 5 of 27
5. Question
If (9)³ is subtracted from the square of a number, the answer so obtained is 567. What is the number?
Hint
Let the required number be x
∴ x² – (9)³ = 567
x² = 567 + 729 = 1296
∴ x =
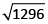= 36 -
Question 6 of 27
6. Question
If (78)² is subtracted from the square of the number, the answer so obtained is 6,460. What is the number?
Hint
Let the number be x.
According to the question,
x² – 78² = 6460
⇒ x² = 6460 + 6084
⇒ x² = 12544
-
Question 7 of 27
7. Question
What is the least number to be added to 4400 to make it a perfect square?
Hint
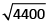= 66.33 ∴ Required number = 67² – 4400
= 4489 – 4400 = 89
⇒ x =
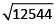= 112 -
Question 8 of 27
8. Question
Which least number shall be added to 8115 to make it a perfect square?
Hint
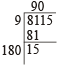
∴ required number = 91 × 91 – 8115 = 166
-
Question 9 of 27
9. Question
What is the least number to be added to 4321 to make it a perfect square?
Hint
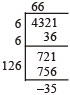
∴ (66)² – 4321 = 4356 – 4321 = 35
-
Question 10 of 27
10. Question
What is the least number to be added to 4700 to make it a perfect square?
Hint
69 × 69 = 4761
68 × 68 = 4624
Clearly, 4624 < 4700 < 4761
∴ Hence, 61 should be added to make = 4761 – 4700 = 61
-
Question 11 of 27
11. Question
What is the least number to be added to 3986 to make it a perfect square?
Hint
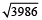= 63.13 ∴ Here, 63² = (64)² – 3986
= 4096 – 3986 = 110
-
Question 12 of 27
12. Question
What is the least number to be added to 1500 to make it a perfect square?
Hint
38² = 1444
39² = 1521
∴ Required number
= 1521 – 1500 = 21
-
Question 13 of 27
13. Question
The difference between two numbers is 3 and the difference between their squares is 63. Which is the larger number?
Hint
Let the larger and smaller numbers be x and y respectively.
Then, x – y = 3 …(i)
and, x² – y² = 63
⇒ (x + y) (x – y) = 63
⇒
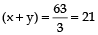…(ii)From equation (i) and (ii),
x = 12
-
Question 14 of 27
14. Question
If (12)³ is subtracted from the square of a number the answer so obtained is 976. What is the number?
Hint
Let the number be x.
x² – (12)3 = 976
∴ x² = 976 + 1728 = 2704
∴ x =
-
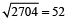
Question 15 of 27
15. Question
If (56)² is added to the square of a number, the answer so obtained is 4985. What is the number?
Hint
Let the number be x.
x² + (56)² = 4985
⇒ x² = 4985 – 3136 = 1849
∴ x =
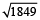= 43 -
Question 16 of 27
16. Question
The difference between a two-digit number and the number obtained by interchanging the two digits of the number is 9. The sum of the digits of the number is 15. What is the product of the two digits of the two-digit number?
Hint
Let the two-digit number be
= 10 x + y, where x < y.
Number obtained after interchanging the digits = 10 y + x
According to the question,
10 y + x – 10 x – y = 9
⇒ 9y – 9x = 9
⇒ 9(y –x) = 9
⇒ y – x = 1 …(i)
and x + y = 15 …(ii)
From equations (i) and (ii),
y = 8 and x = 7
∴ Required product = 8 × 7 = 56
-
Question 17 of 27
17. Question
The number obtained by interchanging the two digits of a two-digit number is less than the original number by 18. The sum of the two digits of the number is 16. What is the original number?
Hint
Let the number be (10x + y)
Then, (10x + y) – (10y + x) = 18
⇒ 9x – 9y = 18
⇒ x – y = 2 …(i)
and, x + y = 16 …(ii)
∴ x = 9, y = 7
From equations (i) and (ii),
So, the number is (10 × 9 + 7) = 97
-
Question 18 of 27
18. Question
How many numbers from 1 to 100 are there each of which is not only exactly divisible by 4 but also has 4 as a digit?
Hint
The numbers from 1 to 100 which are exactly divisible by
4 are 4, 8, 12, 16, 20,24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100.
But each number should have 4 as its digit.
The required numbers are 4, 24, 40, 44, 48, 64, 84.
Clearly, there are 7 such numbers.
-
Question 19 of 27
19. Question
The numbers 1 to 29 are written side by side as follows 1234567891011 … 2829. If the number is divided by 9, then what is the remainder?
Hint
Sum of the digits of the ‘super’ number
= 1 + 2 + 3 +…. + 29
=
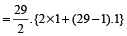
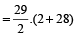
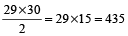
Now, sum of digits in the number 435 = 4 + 3 + 5 = 12 which gives a remainder of 3 when divided by 9.
-
Question 20 of 27
20. Question
If x959y is divisible by 44 and y >5, then what are values of the digit x and y?
Hint
Here 44 = 11 × 4
∴ the number must be divisible by 4 and 11 respectively. Test of 4 says that 9y must be divisible by 4 and since y > 5, so y = 6
Again , x 9596 is divisible by 11,
so x + 5 + 6 = 9 + 9
⇒ x = 7
Thus x = 7, y = 6
-
Question 21 of 27
21. Question
The quotient arising from the division of 24162 by a certain number x is 89 and the remainder is 43. Find x.
Hint
24162 = 89x + 43
⇒ x = (24162 – 43) ÷ 89 = 271
-
Question 22 of 27
22. Question
Find the unit’s digit in the product (2467)¹⁵³ × (341)⁷².
Hint
Clearly, unit’s digit in the given product = unit’s digit in 7¹⁵³ × 1⁷².
Now, 7⁴ gives unit digit 1.
∴ 7¹⁵³ gives unit digit (1 × 7) = 7. Also 1⁷² gives unit digit 1.
Hence, unit’s digit in the product
= (7 × 1) = 7.
-
Question 23 of 27
23. Question
The unit’s digit in the product (7⁷¹×6⁵⁹×3⁶⁵) is:
Hint
Unit digit in 7⁴ is 1.
Unit digit in 7⁶⁸ is 1.
∴ Unit digit in 7⁷¹ = 1 × 7³ = 3
Again, every power of 6 will give unit digit 6.
∴ Unit digit in 6⁵⁹ is 6.
Unit digit in 3⁴ is 1.
∴ Unit digit in 3⁶⁴ is 1.
Unit digit in 3⁶⁵ is 3.
∴ Unit digit in (7⁷¹ × 6⁵⁹ × 3⁶⁵)
= Unit digit in (3 × 6 × 3) = 4.
-
Question 24 of 27
24. Question
How many times must 79 be subtracted from 5 × 10⁴ so as to obtain 43759?
Hint
Let x be the number of times, then
79x + 43759 = 50,000
⇒ x = (50000 – 43759) ÷ 79 = 79
-
Question 25 of 27
25. Question
55³ + 17³ – 72³ is divisible by
Hint
-
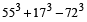
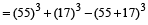
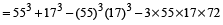
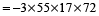
Question 26 of 27
26. Question
The digit in the unit’s place of the number represented by (7⁹⁵ – 3⁵⁸) is:
Hint
Unit digit in 7⁴ is 1. So, unit digit in 7⁹² is 1.
∴ Unit digit in 7⁹⁵ is 3.
Unit digit in 3⁴ is 1.
∴ Unit digit in 3⁵⁶ is 1.
∴ Unit digit in 3⁵⁸ is 9.
∴ Unit digit in (7⁹⁵ – 3⁵⁸) = (13 – 9) = 4.
-
Question 27 of 27
27. Question
What is the digit in the unit place of 2⁵¹?
Hint
The digit in the unit’s place of 2⁵¹ is equal to the remainder when 2⁵¹ is divided by 10. 2⁵ = 32 leaves the remainder 2 when divided by 10. Then 2⁵⁰ = (2⁵)¹⁰ leaves the remainder 2¹⁰ = (2⁵)² which in turn leaves the remainder 2² = 4. Then
2⁵¹ = 2⁵⁰×2, when divided by 10, leaves the remainder 4×2 = 8.