Time limit: 0
Finish Test
0 of 14 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
Information
- Most Important Multiple Choice Questions
- Online LCM and HCF Exercise with Correct Answer Key and Solutions
- Useful for all Competitive Exams
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 14 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- Answered
- Review
- Question 1 of 14
1. Question
The least number of five digits which is exactly divisible by 12, 15 and 18, is:
Hint
Least number of 5 digits is 10,000 L.C.M. of 12, 15 and 18 is 180.
On dividing 10000 by 180, the remainder is 100.
∴ Required number
= 10000 + (180 – 100) = 10080.
- Question 2 of 14
2. Question
The greatest number of four digits which is divisible by 15, 25, 40 and 75 is :
Hint
Greatest number of 4 digits is 9999. L.C.M. of 15, 25, 40 and 75 is 600.
On dividing 9999 by 600, the remainder is 399.
∴ Required number
= (9999 – 399) = 9600.
- Question 3 of 14
3. Question
The least number which should be added to 2497 so that the sum is exactly divisible by 5, 6, 4 and 3 is:
Hint
L.C.M. of 5, 6, 4 and 3 = 60.
On dividing 2497 by 60, the remainder is 37.
∴ Number to be added
= (60 – 37) = 23.
- Question 4 of 14
4. Question
Find the maximum number of students among whom 429 mangoes and 715 oranges can be equally distributed.
Hint
Required number
= HCF of 429 and 715 = 143
- Question 5 of 14
5. Question
Find the greatest number that will divide 115, 149 and 183 leaving remainders 3, 5, 7 respectively.
Hint
Required number
= HCF of (115 – 3), (149 –5) and (183 – 7)
= HCF of 112, 144 and 176 = 16
- Question 6 of 14
6. Question
Find the greatest number which when subtracted from 3000 is exactly divisible by 7, 11, 13.
Hint
Required number
= 3000 – LCM of 7, 11, 13
= 3000 – 1001 = 1999
- Question 7 of 14
7. Question
The L.C.M. of two number is 630 and their H.C.F. is 9. If the sum of numbers is 153, their difference is
Hint
Let numbers be x and y.
Product of two numbers = their (LCM × HCF)
⇒ xy = 630 × 9
Also, x + y = 153 (given)
since x – y
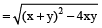
⇒
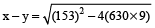
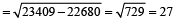
- Question 8 of 14
8. Question
Product of two co-prime numbers is 117. Their L.C.M. should be:
Hint
H.C.F of co-prime numbers is 1.
So, L.C.M. = 117/1 = 117.
- Question 9 of 14
9. Question
What is the smallest number which when increased by 5 is completely divisible by 8, 11 and 24?
Hint
Required number
= LCM of ( 8, 11, 24 ) – 5
= 264 – 5 = 259
- Question 10 of 14
10. Question
If the L.C.M and H.C.F. of two numbers are 2400 and 16, one number is 480; find the second number.
Hint
Product of numbers
= (LCM × HCF)
⇒ 480 × second number = 2400 × 16
⇒ second number = 80
- Question 11 of 14
11. Question
The LCM of two numbers is 4800 and their HCF is 160. If one of the numbers is 480, then the other number is :
Hint
Product of numbers = HCF × LCM
⇒ The other number
=
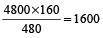
- Question 12 of 14
12. Question
The LCM of two numbers is 280 and their ratio is 7 : 8. The two numbers are :
Hint
Let the numbers be 7x and 8x.
⇒ Their HCF = x
Now, LCM × HCF = Product of Numbers
i.e. 280 × x = 56x²
⇒ x = 5
Hence, the numbers are 35 and 40.
- Question 13 of 14
13. Question
The LCM and HCF of two numbers are 84 and 21, respectively. If the ratio of two numbers be 1 : 4, then the larger of the two numbers is :
Hint
Let the numbers be x and 4x.
Then, 84 × 21 = x × 4x
⇒ 4x² = 1764
⇒ x² = 441
⇒ x = 21
⇒ 4x = 4 × 21 = 84
Thus the larger number = 84
- Question 14 of 14
14. Question
How many numbers, between 1 and 300 are divisible by 3 and 5 together?
Hint
LCM of 3 and 5 = 15
∴ 300/15 = 20 numbers
