Time limit: 0
Finish Test
0 of 19 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
Information
- Most Important Multiple Choice Questions
- Online Geometry Exercise with Correct Answer Key and Solutions
- Useful for all Competitive Exams
You have already completed the quiz before. Hence you can not start it again.
Test is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 19 questions answered correctly
Time has elapsed
You have reached 0 of 0 points, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- Answered
- Review
- Question 1 of 19
1. Question
Two circles touch each other internally. Their radii are 2 cm and 3 cm. The biggest chord of the outer circle which is outside the inner circle is of length
Hint
AB =
∴ AC =
cm - Question 2 of 19
2. Question
Two circles of radii 10 cm. 8 cm. intersect and length of the common chord is 12 cm. Find the distance between their centres.
Hint
Here, OP = 10 cm; O’P = 8 cm
PQ = 12 cm
∴ PL = 1/2 PQ
⇒ PL = ½ × 12
⇒ PL = 6 cm
In rt. ∆ OLP, OP² = OL² + LP²
(using Pythagoras theorem)
⇒ 10² = OL² + 6²
⇒ OL² + 64; OL = 8
In ∆ O'LP, (O'L)² = O'P² – LP²
= 64 – 36 = 28
O’L² = 28
O’L = 5.29 cm
∴ OO'= OL + O'L
OO'= 13.29 cm
- Question 3 of 19
3. Question
Arc ADC is a semicircle and DB ⊥ AC. If AB = 9 and BC = 4, find DB.
Hint
m ∠ ADC = 90⁰ (Angle subtended by the diameter on a circle is 90°)
∴ ∆ ADC is a right angled triangle.
∴ (DB)² = BA × BC
[since, DB is the perpendicular to the hypotenuse]
= 9 × 4 = 36
∴ DB = 6
- Question 4 of 19
4. Question
A point P is 13 cm. from the centre of a circle. The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle.
Hint
Tangent at any point of a circle is ⊥ to the radius
In ∆OPT, OP² = PT² + OT²
(13)² = (12)² + OT²
⇒ 169 – 144 =OT²
⇒ 25 = OT²
⇒ 5 = OT
- Question 5 of 19
5. Question
In the figure given below, O is the centre of the circle. If ∠OBC = 37°, then ∠BAC is equal to :
Hint
We have, ∠OBC = ∠OCB = 37°
(equal angles of an isosceles triangle)
⇒ ∠COB = 180° – (37° + 37°) = 106°
Therefore, ∠BAC
- Question 6 of 19
6. Question
PQRS is a square. SR is a tangent (at point S) to the circle with centre O and TR=OS. Then, the ratio of area of the circle to the area of the square is
Hint
In
∴
- Question 7 of 19
7. Question
In the given figure, AB is chord of the circle with centre O, BT is tangent to the circle. The values of x and y are
Hint
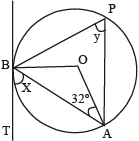
Given AB is a circle and BT is a tangent,
∠BAO = 32°
Here, ∠ OBT = 90°
[Since tangent is ⊥ to the radius at the point of contact]
OA = OB [ Radii of the same circle ]
∴ ∠ OBA = ∠OAB = 32° [ Angles opposite to equal side are equal]
∴ ∠ OBT = ∠ OBA + ∠ ABT = 90°
⇒ 32° + x = 90°.
⇒ ∠ x = 90° – 32° = 58° .
Also, ∠ AOB = 180° – ∠OAB – ∠OBA
= 180° – 32° – 32° = 116°
Now Y = ½ AOB [ Angle formed at the center of a circle is double the angle formed in the remaining part of the circle] = ½ × 116° = 58° .
- Question 8 of 19
8. Question
In the figure given below, AB is a diameter of the semicircle APQB, centre O, ∠ POQ = 48° cuts BP at X, calculate ∠AXP.
Hint
b = ½(48°) (∠at centre = 2 at circumference on same PQ) = 24°
∠AQB = 90° (∠In semi- circle)
∠QXB = 180° – 90° – 24° = 66°
- Question 9 of 19
9. Question
OA is perpendicular to the chord PQ of a circle with centre O. If QR is a diameter, AQ = 4 cm, OQ = 5 cm, then PR is equal to
Hint
AO =
=
= 
= 3Now, from similar ∆s QAO and QPR
OR = 2OA = 2× 3 = 6 cm.
- Question 10 of 19
10. Question
In the given figure, m ∠ EDC = 54°. m ∠ DCA = 40°.Find x, y and z.
Hint
m ∠ ACD = ½ M(are CXD) = m ∠ DEC
∴ m ∠ DEC = x = 40°
∴ m ∠ ECB = ½ m (are EYC) = m ∠ EDC
∴ m ∠ ECB = y = 54°
54 + x + z = 180° [Sum of all the angles of a triangle]
54 + 40 + z = 180°
∴ z = 86°.
- Question 11 of 19
11. Question
ABCD is a cyclic quadrilateral in which BC || AD, ∠ADC = 110° and ∠BAC = 50° find ∠DAC
Hint
∠ABC + ∠ADC = 180° (sum of opposites angles of cyclic quadrilateral is 180°)
⇒ ∠ABC + 110° = 180° [ABCD is a cyclic quadrilateral]
⇒ ∠ABC = 180 – 110
⇒ ∠ABC = 70°
Since AD || BC
∴ ∠ABC + ∠BAD = 180° [Sum of the interior angles on the same side of transversal is 180°]
70° + ∠ BAD = 180°
⇒ ∠BAD = 180° – 70° = 110°
⇒ ∠BAC + ∠DAC = 110°
⇒ 50° + ∠DAC = 110°
⇒ ∠DAC = 110° – 50 ° = 60°
- Question 12 of 19
12. Question
In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If length of one chord is 16 cm, then the length of the other one is :
Hint
Let PQ and RS be two parallel chords of the circle on the opposite sides of the diameter AB and PQ = 16 cm
Now, PN = 8 (Since ON is the perpendicular bisector)
In ∆ PON, ON² = OP² – PN²
= (17)² – (8)² = 289 – 64 = 225
⇒ ON = 15
∴ OM = 23 – 15 = 8
In ∆ ORM, RM² = OR² – OM²
= (17)² – (8)² = 289 – 64 = 225
⇒ RM = 15
⇒ RS = 15 × 2 = 30 cm
- Question 13 of 19
13. Question
In given fig, if ∠BAC = 60° and ∠BCA = 20° find ∠ADC
Hint
In ∆ABC, ∠B = 180° – ( 60° + 20°) [By ASP]
⇒ ∠B = 100°
But ∠B + ∠D = 180°
[Since ABCD is a cyclic quadrilateral; Sum of opposite is 180°]
100° + ∠D = 180°
⇒ ∠ADC = 80°
- Question 14 of 19
14. Question
A point P is 26 cm. away form the centre O of a circle and the length PT of the tangent draw from P to the circle is 10cm. Find radius of the circle
Hint
24 cm
- Question 15 of 19
15. Question
In a circle of radius 10 cm, a chord is drawn 6 cm from its centre. If an another chord, half the length of the original chord were drawn, its distance in centimeters from the centre would be:
Hint
In a triangle ∆AMO,
= 8Therefore, the length of the another chord A’B′ = 8 cm.
Now, A’N = 4
In ∆ OA’N, ON² = (OA’)² – A’N²
= 10² – 4² = 100 – 16 = 84
⇒ ON =
- Question 16 of 19
16. Question
AB and CD two chords of a circle such that AB = 6 cm, CD = 12 cm. And AB || CD. The distance between AB and CD is 3 cm. Find the radius of the circle.
Hint
Draw OE ⊥ CD and OF ⊥ AB
AB||CD [Given]
Let ‘r’ be the radius of the circle
Now in rt. ∆ OED, (OD)² = (OE)² + (ED)²
[using Pythagoras theorem]
⇒ r² = x² + 36 …(1)
In rt. ∆ OFB, (OB)² = (OF)² + (EB)²
⇒ r² = (x + 3)² + (3)²
⇒ r² = x² + 6x + 9 + 9
⇒ r² = x² + 6x + 18 …(2)
From (1) and (2), we get
x² + 36 = x² + 6x + 18
⇒ 36 = 6x + 18
⇒ 36 – 18 = 6x
⇒ 6x = 18
⇒ x = 3
For (1), r² = (3)² + (6)²
r² = 9 + 36
⇒ r² = 45
cm - Question 17 of 19
17. Question
A circle with radius 2 is placed against a right angle. Another smaller circle is also placed as shown in the adjoining figure. What is the radius of the smaller circle?
Hint
OABC is square with side = 2
OB = 2
= OD + r + O’B = 2 + r + r
⇒ r(
+1) = 2(
–1)
- Question 18 of 19
18. Question
In the figure below, which of the following is the relationship between ‘x’ and ‘y’ if the equal circles shown are tangents to each other and to the sides of the rectangle
Hint
Diameter of circle = x
∴ y = 4x
∴ x = ¼ y
- Question 19 of 19
19. Question
In the cyclic quadrilateral ABCD BCD =120° , m(arc DZC) = 7°, find DAB and m (arc CXB).
Hint
m ∠ DAB + 180° – 120° =60°
[Opposite angles of a cyclic quadrilateral]
m (arc BCD) = 2m ∠ DAB = 120°.
∴ m (arc CXB) = m (BCD) – m (arc DZC) = 120° – 70° = 50° .