Puzzle Test Reasoning

Puzzle Test Tricks, Examples and Online Test

In this chapter you will see some typical problems in which you would be given a series of interlinked information and on the basis of those informations you would be expected to reach certain conclusions.

In this type of questions, we have to analyse the given information and condense it in a suitable form to answer the questions. Though there exists no set formula to solve this kind of problems, yet a systematic approach can help to solve questions.

Type of Questions

1. Problems Based On Comparison

In such problems comparison of different objects or persons has to be made. Such comparisons are done on the basis of marks, ages heights, etc.
Let us see the following examples:

Directions: Read the informations given below to answer the given questions:

(i) 7 students A, B, C, D, E, F and G take a series of tests.
(ii) No two students obtain the same marks.
(iii) G always scores more than A.
(iv) A always scores more than B.
(v) Each time either C scores the highest and E gets the least, or alternatively D scores the highest and F or B scores the least.

Question 1. If D is ranked 6th and B is ranked 5th, which of the following can be true?

G is ranked 1st or 4th
C is ranked 2nd or 3rd
A is ranked 2nd or 5th
F is ranked 3rd or 4th
E is ranked 4th or 5th.

Question 2. If C gets most, G should be ranked not lower than_____

2nd
3rd
4th
5th
6th.

Question 3. If C is ranked 2nd and B is ranked 5th, which of the following must be true?

D is ranked 3rd
E is ranked 6th
A is ranked 6th
G is ranked 4th
F is ranked 6th.

Question 4. If D is ranked 2nd, which of the following can be true?

F gets more than G
G gets more than D
A gets more than C
A gets more than G
E gets more than B

Question 5. If G is ranked 5th, which of the following must be true?

D scores the highest
C is ranked 2nd
E is ranked 3rd
B is ranked 4th
F scores the least

Solutions (Q. 1-5): If you give a serious look to the problem you will find that such problems are as same as the arrangement problems. Therefore, we have to go like arrangement problem while solving problems based on comparison.

In this case, we see there is no definite information. Sentence 5 gives a definite information but it is conditional. Still, we draw all the possibilities based on sentence (v).

(1) C __ __ __ __ __ __ E

or (2) D __ __ __ __ __ __ F

or (3) D __ __ __ __ __ __ B

We see that the two additional informations (iii) and (iv) are inadequate to reach a definite conclusion. Hence, keeping these in mind. We move on to the given questions.

1. D is ranked 6th and B is 5th. This does mean that possibilities (2) and (3) are violated. Hence, possibility (i) must be true. Thus, we have:

C __ __ __ B D E

Also by virtue of (iii) and (iv) we can have only one arrangement for G, A and B which is GAB. Accordingly, there are three possibilities:

F G A F B D E

or C G F A B D E

or C F G A B D E

∴ Correct answer is (4)

2. Just see the analysis of previous question.

∴ Correct answer is (3)

3. G is ranked 2nd does mean possibility (1) is false. Therefore, possibilities (2) and (3) remain. Now, B is ranked 5th does mean possibility (3) is false.

Hence, possibility (2) remains:

D C __ __ B __ F

Now, by virtue of (iii) and (iv), we must have G and A before B in that order. Consequently the 6th place would go to the only letter remaining that is E.

Hence, D C G A B E F

∴ Correct answer: 2.

4. D is ranked 2nd does mean possibilities (2) and (3) are false. Hence possibility (1) is true. Now look at the analysis of Question (1) and you will get the correct answer as: 1.

5. If G is ranked 5th, we can not definitely say which among the three possibilities (1), (2) and (3) are true or false. But sentences (iii) and (iv) definitely imply that the position of A will be 6th and that of B seventh. Now if B is 7th, it does mean that possibility (3) is true. Hence, we have

D ? ? ? G A B.

∴ Correct answer is (1)

2. Problems based on Blood Relations and Profession

Such problems are very much similar to the problems related to blood relation. What makes it different is the addition of new data– the professions of family members. You will get the more clear idea about this type of problem. Let us see the example given below:

Directions: Read the following information carefully and answer the questions given below it:

(i) A, B, C, D, E and P are members of a family.
(ii) There are two married couples.
(iii) B is an engineer and the father of E.
(iv) P is the grandfather of C and is a lawyer.
(v) D is the grandmother of E and is a housewife.
(vi) There is one engineer, one lawyer, one teacher, one housewife and two students in the family.

Question 6. Who is the husband of A?

Question 7. Which of the following are two married couple?

PD, BA
PD, BE
PD, CA
ED, CP
None of these

Question 8. Which of the following is definitely a group of male members?

B, P, E
P, E
B, P, A
B, P
None of these

Question 9. Who is the sister of E?

C
D
A
Data inadequate
None of these

Question 10. What is the profession of A?

Housewife
Engineer
Teacher
Engineer or Teacher
Housewife or Teacher

Solutions (Qs 6-10): Here, (i), (ii), and (iv) are useful secondary informations. While (iii), (iv) and (v) are the actual informations. We start with the 3rd sentence because it mentions a parent. Child relationship its diagram can be made as the following:

Now, we move on to another sentence that involves either B or E. You see that the 5th sentence gives some information about E. It says that D is the grandmother E. Point to be noted that if D is the grandmother of E, then the son of D must be father of E and hence B is the son of D. Now, the diagram takes the following form.

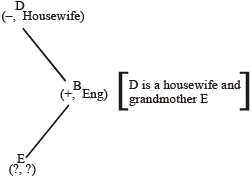
Now, the 4th sentence has the remaining information and diagram for it is given below:

Now, we see that we have ended up with two different component. Then how to resolve this deadlock? The answer is simple— to resolve it we make used of the given useful secondary information (USI).

“There are two married couple in the family.” Clearly, the two possible pairs are of grandfather, grandmother and father, mother. Therefore, we combine the two diagrams into the following way.

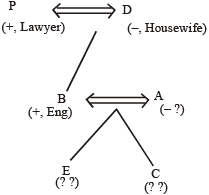
Point to be noted that the professions of A, E and C are yet unknown. However, with reasonable justification, we may assume that the mother (A) should be the teacher and the two children E and C should be students. But this conclusion can be challenged and has no reason at all.

Apart from that the sexes of E and C can not be determined.

Now, read the question and check your answer one by one:

6. (3)

7. (1)

8. (4)

9. (4)

10. (3)

3. Problems based on Conditional Selection

In this type of problems, a group of objects/persons has to be selected from a given larger group, as per the given restrictions. You will get the better idea of such type of problem from the problem given below:-

Directions: Study the following information carefully and answer the questions given below:

From, amongst 6 boys J, K, L, M, N, and O and 5 girls P, Q, R, S and T, a team of 6 is to be selected under the following conditions:
(i) J and M have to be together.
(ii) L can not go with S.
(iii) S and T have to be together.
(iv) K can not be teamed with N.
(v) M cannot go with P.
(vi) K and R have to be together.
(vii) L and Q have to be together.

Question 11. If there be 5 boys in the team, the lone girl member is:

P
Q
R
S
None of these

Question 12. If including P, the team has three girls, the members other than P are:

K L OR Q
JMNST
JMKST
KORST
None of these

Question 13. If, the team including L consists of 4 boys the members of the team other than L are:

JMNPQ
JKMQR
MNOJQ
KNORQ
None of these

Question 14. If 4 members including N, have to be boys, the members other than N are:

JKLQR
JMOST
KLOQR
JLMOQ
None of these.

Question 15. If 4 members have to girls, the members of the team are:

KLPQRS
KOPRST
KLQRST
KLPQRT
None of these

Solutions (Qs 11-15): Solving problems like example 6 is very easy. Make the group of all the pairs that have to be together on one side and the pairs that must not be together on the other side. Next, read each of the questions and treat that as an additional information. Finally analyse the possibilities and choose the possibilities that satisfies all the conditions. Let us see the process below:

1stly, we can summarise the conditions in the following way:

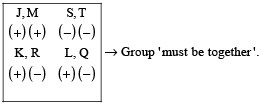
Group never be together

L, S	K, N	M, P
(+)(–)	(+)(+)	(+)(–)

Now we move on to questions one by one.

11. Here, number of boys are 5. We see that K and N can never be together. Therefore, there are only two ways of selecting 5 boys – JKLMO and JNLMO. But the possiblity is not possible because if K would go then R should also go, and if L goes than Q should also go. Hence, JNLMO is the only possibility in which L’s friend Q would be the lone girl member.

∴ Correct answer choice is (2).

12. There are three girls including P. P is there, so M must not be there. If M is not there, J would not be there. So two boys J and M are eliminated. Since, the team should have only 6 members, hence there should be three boys. Two boys J and M are eliminated. Therefore, the possibilities of selecting three boys are : KLN, KLO, KNO, LNO. But K and N can’t be together. Hence the remaining possibilities are KLO and LNO. Now, K must be with R and L must be with Q. Therefore, we have PKRLQO and PLQNO. To the 2nd possibility we need to add a girl. We can’t add R since R can’t go without K. We can’t add T since T can’t go without s. Conversely, we can’t add S either. Hence, this possibility is also eliminated. This, the only possible choice remains PKRLQO.

∴ correct answer choice is (1).

Quicker method:

Start with the answer choices. Choice (2) and choice (3) have M in them. M can’t go as P is there. Choice (4) is not correct as it has more than three girls including P. Hence, the correct answer choice must be either (1) or (3). But on verifying we see that a is indeed the correct choice as it does not violate any restriction.

∴ Correct answer choice is (1).

13. There are 4 boys including L. So there must be two girls. Now if L is present, S can’t go and if S can’t go, T won’t go. Hence, three girls remain– P, Q and R out of these, two can be selected in the ways given below:

PQ, PR, and QR.

Now, if P is selected, M can’t go and if M can’t go, J will not go. In such case the team would have to include K and N as 4 boys hence to be selected. But K and N can’t be together. This means that P should not be selected. Therefore, the only possibility of selecting two girls is QR. But R means the necessary inclusion of K, which in turn means necessary inclusion of N. Hence, the possible combination is LKQR. To this we should add two boys out of J, M and O. The only possibility is adding J and M as neither of these would go without the other. Hence, the team is JMLKQR.

∴ Correct answer choice is (2).

Quicker method

Choice (1) is incorrect as it has M and P together. Choice (3) is incorrect as it has only one girl. Choice (4) is incorrect as it has K and N together. Hence, two choices (2) and (5) remain. On verifying we see that (2) is the correct answer choice.

14. Inclusion of N ⇒ Exclusion of K ⇒ Exclusion R. Four boys does mean there should be two girls. How do you select 2 girls out of P, Q, S and T if S and T have always to be together? The only two possible way are –P, Q, and S, T. If we choose P we can’t select M, and hence we can’t select J either. This means the exclusion of J and M in addition to that of K. Since, this is not possible in order to have four boys, we must not select P. Hence, we select S.T. Now,
selecting S means excluding L. Hence, K and L are excluded.

The team would be– JMNOST

∴ Correct answer choice is (2).

Quicker method

Choices (1) and (3) are wrong as they have L and S together choice (4) is wrong as it does not have S and T together.

∴ the (2) and (5) are remaining choices. But on verifying, we find that option (2) is the correct answer choice.

Solved Examples

So far, an exhaustive pattern and types of problems have been covered in our study of problem solving. But sometimes you see the kind of problems which are not as same as the problems, we have discussed so far. In fact such questions, are a wide of various categories studied till now. For example, you may have profession-problems outside a family, or you may have blood relations and arrangement problems mixed into each-other. In fact, such problems come before you as a surprise and try to puzzle you in various ways.

Let us see a miscellaneous type of problem given below:

Directions: Study the following information and answer the questions given below it:

L, M, N, O and T are five persons. One is a cricket players, one is a chess player and one is a football player. L and O are unmarried ladies and do not participate in any game. None of the ladies plays chess or football. There is a married couple in which T is the husband. M is the brother of N and is neither a chess player nor a cricket player.

Question 16. Who is the football player?

Question 17. Who is the cricket player?

Question 18. Who is the chess player?

Question 19. Who is the wife of T?

L
M
N
O
Data inadequate

Question 20. The three ladies are:

L, M and N
M, N and O
L, M and O
L, N and O
None of these

Solutions (Qs 16-20): Here, we see that many dimensions attached to each individual in this problem. The dimensions are sex marital status and favourite sport.

Let us take them one by one.

Gender: L and O are females. T is a husband, so he must be a male. M is a brother and hence he must be a male. The one remaining is N. Since T is a husband and since the two ladies L and O are unmarried, N must be the wife of T. Hence, N is a female.
Marital status: L and O are unmarried. N and T are married to each other.
Favourite Sport: L and O do not play any game. Out of the remaining three, one plays football, another chess and another cricket. N is a lady and no lady plays football or chess. Hence, N plays cricket. M plays neither chess nor cricket. Hence, M must be playing football. Hence, T plays the only remaining sport chess.

Now you can check the questions one by one:

16. (2)

17. (3)

18. (3)

19. (3)

20. (4)

NEXT: Puzzle Test Exercise