The clock has 12 hours numbered from 1 to 12. Also, the clock is divided into 60 equal minute divisions. Therefore, each hour number is separated by five minute divisions.
If a watch or a clock indicates 8.15, when the correct time is 8, it is said to be 15 minutes too fast. On the other hand, if it indicates 7.45, when the correct time is 8, it is said to be 15 minutes too slow.
Minute Spaces
The face or dial of watch is a circle whose circumference is divided into 60 equal parts, called minute spaces.
Hour Hand and Minute Hand
A clock has two hands, the smaller one is called the hour hand or short hand while the larger one is called minute hand or long hand.
Relative position of the hands
The position of the M.H. relative to the H.H. is said to be the same, whenever the M.H. is separated from the H.H. by the same number of minute divisions and is on same side (clockwise or anticlockwise) of the H.H. Any relative position of the hands of a clock is repeated 11 times in every 12 hours.
- When both hands are 15 minute spaces apart, they are at right angle.
- When they are 30 minute spaces apart, they point in opposite directions.
- The hands are in the same straight line when they are coincident or opposite to each other.
Incorrect Clock
If a clock indicates 6 : 10, when the correct time is 6 : 00, it is said to be 10 minute to fast and if it indicates 5 : 50 when the correct time is 6 : 00, it is said to be 10 minute slow.
If both hands coincide at an interval x minutes and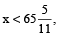 
then total time gained
and clock is said to be ‘fast’.
If both hands coincide at an interval x minutes and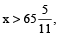 
then total time lost 
and clock is said to be ‘slow’.
Points to Remember
One minute division =
= 6° apart. i.e. In one minute, the minute hand moves 6°.
One hour division = 6° × 5 = 30° apart. i.e. In one hour, the hour hand moves 30° apart.
Also, in one minute, the hour hand moves =
=
apart.
Since, in one minute, minute hand moves 6° and hour hand moves
, therefore, in one minute, the minute hand gains
more than hour hand.
In one hour, the minute hand gains
over the hour hand. i.e. the minute hand gains 55 minutes divisions over the hour hand.
In every hour, both the hand coincide once.
In a day, the hands are coinciding 22 times.
In every 12 hours, the hands of clock coincide 11 times.
In every 12 hours, the hands of clock are in opposite direction 11 times.
In every 12 hours, the hands of clock are at right angles 22 times.
In every hour, the two hands are at right angles 2 times.
In every hour, the two hands are in opposite direction once.
In a day, the two hands are at right angles 44 times.
If both the hands coincide, then they will again coincide after
minutes. i.e. in correct clock, both hand coincide at an interval of
minutes.
If the two hands coincide in time less than
minutes, then clock is too fast and if the two hands coincides in time more than
minutes, then the clock is too slow.
Solved Examples
Question 1. Find the angle between the minute hand and hour hand of a clock when the time is 7.20
Solution: Angle traced by hour hand in 12 hours = 360 Degrees
Angle traced by it in 7 hrs 20 min i.e 22/3 hrs
= (360/12) × (22/3)= 2200
Angle traced by minute hand in 60 min = 3600
Angle traced by it in 20 minutes = (360/60) × 20 = 1200
Required angle = (2200 – 1200) = 1000
Question 2. At what time between 2 and 3 o’ clock will the hands of a clock together ?
Solution: At 2 o’ clock, the hour hand is at 2 and minute hand at 12, i.e., they are 10 minute spaces apart.
To be together , the minute hand must gain 10 minutes over the hour hand.
Now, 55 minutes are gaines by it in 60 minutes
10 minutes will be gained in {(60/55) × 10} min =10 10/11 min
The hands will coincide at 10 10/11 min past 2
Question 3. At what time between 4 and 5 o’ clock will the hands of a clock be at right angle ?
Solution: At 4 o’ clock, the minute hand will be 20 min spaces behind the hour hand.
Now , when the two hands are at right angles, they are 15 min. spaces apart.
So, they are at right angles in following two cases
Case I: When minute hand is 15 minute spaces behind the hour hand
In this case min hand will have to gain (20 –15) = 5 minute spaces
55 min. spaces will be gained by it in (60 × 5)/55 min = 5 5/11 min
They are at right angles at 5 5/1 min past 4
Case II: When the minute hand is 15 minute spaces ahead of the hour hand
They are at right angles at 38 2/11 min past 4
Question 4. At what time between 4 and 5 will the hands of a watch
(i) coincide, and (ii) point in opposite directions.
Solution:
(i) At 4 O’ clock, the hands are 20 minutes apart. Clearly the minute hand must gain 20 minutes before two hands can be coincident.
But the minute-hand gains 55 minutes in 60 minutes.
Let minute hand will gain x minute in 20 minutes.
So,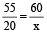 
⇒ 
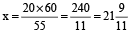min.
∴ The hands will be together at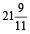 
min past 4.
(ii) Hands will be opposite to each other when there is a space of 30 minutes between them. This will happen when the minute hand gains (20 + 30) = 50 minutes.
Now, the minute hand gains 50 min in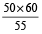 
or 
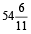min.
∴ The hands are opposite to each other at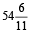 
min past 4.
Question 5. What is the angle between the hour hand and minute hand when it was 5 : 05 pm.
Solution: 5.05 pm means hour hand was on 5 and minute hand was on 1, i.e. there will be 20 minutes gap.
∴ Angle = 20 × 6° = 120° [1 minute = 6°]
Question 6. My watch, which gains uniformly, is 2 min slow at noon on Sunday, and is 4 minutes 48 seconds fast at 2 pm on the following Sunday. When was it correct ?
Solution: From Sunday noon to the following Sunday at 2 pm
= 7 days 2 hours = 170 hours.
The watch gains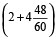
= 
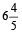minutes in 170 hours.
∴ The watch gains 2 minutes in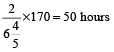 
Now, 50 hours = 2 days 2 hours.
2 days 2 hours from Sunday noon = 2 pm on Tuesday.
Question 7. The minute hand of a clock overtakes the hour hand at intervals of 65 minutes of the correct time. How much a day does the clock gain or lose?
Solution: In a correct clock, the minute hand gains 55 min. spaces over the hour hand in 60 minutes.
To be together again, the minute hand must gain 60 minutes over the hour hand.
55 min. are gained in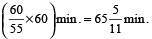 
But, they are together after 65 min.
∴ Gain in 65 min. 
Gain in 24 hours 
∴ The clock gains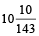 
minutes in 24 hours.
Question 8. A man who went out between 5 or 6 and returned between 6 and 7 found that the hands of the watch had exactly changed place. When did he go out?
Solution: Between 5 and 6 to 6 and 7, hands will change place after crossing each other one time. i.e., they together will make 1 + 1 = 2 complete revolutions.
H.H. will move through
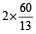or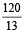 
minute divisions.
Between 5 and 6 →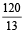 
minute divisions.
At 5, minute hand is 25 minute divisions behind the hour-hand.
Hence it will have to gain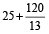 
minute divisions on the hour-hand
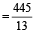minute divisions on the hour hand.
The minute hand gains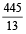 
minute divisions
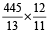minutes 
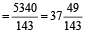minutes
∴ The required time of departure is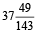 
min past 5.
Calendar
The Julian calendar is a reform of the Roman calendar introduced by Julius Caesar in 46 BC (708 AUC). It took effect the following year, 45 BC (709 AUC), and continued to be used as the civil calendar in some countries into the 20th century. The calendar has a regular year of 365 days divided into 12 months, as listed in Table of months. A leap day is added to February every four years. The Julian year is, therefore, on average 365.25 days long.
The calendar year was intended to approximate the tropical (solar) year. Although Greek astronomers had known, at least since Hipparchus, that the tropical year was a few minutes shorter than 365.25 days, the calendar did not compensate for this difference. As a result, the calendar year gained about three days every four centuries compared to observed equinox times and the seasons. This discrepancy was corrected by the Gregorian reform, introduced in 1582.
The Julian calendar has been replaced by the Gregorian calendar in all countries which formerly used it as the civil calendar. Most Christian denominations have also replaced it with the Gregorian calendar as the basis for their liturgical calendars.
Points to Remember
Odd Days
We are supposed to find the day of the week on a given date. For this, we use the concept of ‘odd days’.In a given period, the number of days more than the complete weeks are called odd days.
Leap Year
- Every year divisible by 4 is a leap year, if it is not a century.
- Every 4th century is a leap year and no other century is a leap year.
Note: A leap year has 366 days.
Examples:
- Each of the years 1948, 2004, 1676 etc. is a leap year.
- Each of the years 400, 800, 1200, 1600, 2000 etc. is a leap year.
- None of the years 2001, 2002, 2003, 2005, 1800, 2100 is a leap year.
Ordinary Year
The year which is not a leap year is called an ordinary years. An ordinary year has 365 days.
Counting of Odd Days
- 1 ordinary year = 365 days = (52 weeks + 1 day.)
- 1 ordinary year has 1 odd day.
- 1 leap year = 366 days = (52 weeks + 2 days)
- 1 leap year has 2 odd days.
- 100 years = 76 ordinary years + 24 leap years = (76 × 1 + 24 × 2) odd days = 124 odd days. = (17 weeks + 5 days) = 5 odd days.
- Number of odd days in 100 years = 5.
- Number of odd days in 200 years = (5 × 2)→ 3 odd days.
- Number of odd days in 300 years = (5 × 3) → 1 odd day.
- Number of odd days in 400 years = (5 × 4 + 1)→ 0 odd day.
- Similarly, each one of 800 years, 1200 years, 1600 years, 2000 years etc. has 0 odd days.
Day of the Week Related to Odd Days:
| No. of days: | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Day: | Sun. | Mon. | Tues. | Wed. | Thurs. | Fri. | Sat. |
Solved Examples
Question 1. What day of the week was 15th August 1949?
Solution: 15th August 1949 means
1948 complete years + first 7 months of the year 1949 + 15 days of August.
1600 years give no odd days.
300 years give 1 odd day.
48 years give {48 + 12} = 60 = 4 odd days.
[For ordinary years → 48 odd days and for leap year 1 more day (48 ÷ 4) = 12 odd days;
60 = 7 × 8 + 4]
From 1st January to 15th August 1949
Odd days : January – 3; February – 0; March – 3; April – 2; May – 3; June – 2; July – 3; August – 1
17 ⇒ 3 odd days.
∴ 15th August 1949 → 1 + 4 + 3 = 8 = 1 odd day.
This means that 15th Aug. fell on 1st day.
Therefore, the required day was Monday.
Question 2. How many times does the 29th day of the month occur in 400 consecutive years?
Solution: In 400 consecutive years, there are 97 leap years.
Hence, in 400 consecutive years, February has the 29th day 97 times and the remaining eleven months have the 29th day
400 × 11 = 4400 times
∴ The 29th day of the month occurs
(4400 + 97) or 4497 times.
Question 3. Today is 5th February. The day of the week is Tuesday. This is a leap year. What will be the day of the week on this date after 5 years?
Solution: This is a leap year. So, next 3 years will give one odd day each. then leap year gives 2 odd days and then again next year give 1 odd day.
Therefore (3 + 2 + 1) = 6 odd days will be there.
Hence the day of the week will be 6 odd days beyond Tuesday, i.e., it will be Monday.
Question 4. What day of the week was 20th June 1837?
Solution: 20th June 1837 means 1836 complete years
+ first 5 months of the year 1837 + 20 days of June.
1600 years give no odd days.
200 years give 3 odd days.
36 years give (36 + 9) or 3 odd days.
1836 years give 6 odd days.
From 1st January to 20th June there are 3 odd days.
Odd days : January — 3; February — 0; March — 3; April — 2; May — 3; June — 6
Total odd days =17 ⇒ 3 odd days.
Therefore, the total number of odd days = (6 + 3) or 2 odd days.
This means that the 20th of June fell on the 2nd day commencing from Monday.
Therefore, the required day was Tuesday.
Question 5. Prove that the calender for 1990 will same for 2001 also.
Solution: It is clear that the calender for 1990 will same for 2001 if first January of both the years is the same weekdays. For that the number of odd days between 31st December 1989 and 31st December 2000 must be zero. Odd days are as given below:
| Year | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 |
| Odd days | 1 | 1 | (L) 2 | 1 | 1 | 1 |
| Year | 1996 | 1997 | 1998 | 1999 | 2000 | |
| Odd days | (L) 2 | 1 | 1 | 1 | (L) 2 |
Total number of odd days = 14 ⇒ 0 odd days.