Average Exercise 1

Required average

=

Required average

=

=

Required average

=

= = 175

Required average

=

= = 493

Required average

=

= = 349

25a + 25b = 115

∴ Average of a and b =

16a + 16b = 672

or, 16 (a + b) = 672

∴ a + b = = 42

Required average =

= = 21

37a + 37b = 5661

⇒ 37(a + b) = 5661

⇒ a + b = = 153

∴ Average = = 76.5

Given,

⇒ 82 × 5 = 410 + 5x ⇒ 410 – 410 = 5x ⇒ x = 0

∴ Required mean is,

Let the other number is N.

Then,

⇒ N = 2XY – X

Let the five consecutive even numbers be

x, x + 2, x + 4, x + 6 and x + 8 respectively.

According to the question,

x + x + 2 + x + 4 + x + 6 + x + 8

= 5 × 52

⇒ 5x + 20 = 260

⇒ 5x = 260 – 20

⇒ x = 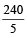= 48

∴ B = x + 2 = 48 + 2 = 50 and

E = x + 8 = 48 + 8 = 56

∴ B × E = 50 × 56 = 2800

Let the consecutive odd numbers be

x, x + 2, x + 4, x + 6 and x + 8

According to the question.

= 41

⇒ 5x + 20 = 41 × 5 = 205

⇒ 5x = 205 – 20 = 185

∴ x = = 37

∴ A = 37 and E = 37 + 8 = 45

Required product = 37 × 45 = 1665

Let A = x,

According to the question,

A + B + C + D + E

= x + (x + 2) + (x + 4) + (x + 6) + (x 8)

⇒ 5x + 20 = 34 × 5 = 170

⇒ B × D = 32 × 36 = 1152

Let the four consecutive odd numbers be

2x – 3, 2x – 1, 2x + 1 and 2x + 3.

Now, 2x = 12 or, x = 6

Lowest odd no. = 2 × 6 – 3 = 9

Suppose the consecutive odd numbers are:

x, x + 2, x + 4, x + 6 and x + 8

Therefore, the required difference = x + 8 – x = 8

Note that answering the above question does not require the average of the five consecutive odd numbers.

Let the three consecutive odd numbers be

x – 2, x, x + 2 respectively.

According to question,

∴ 3x – x + 2 = 42 ⇒ 2x = 40

∴ x = 20 = an even number, which goes against our supposition.

Let the four consecutive even number be

2x, 2x + 2, 2x + 4 and 2x + 6 respectively.

Required difference = 2x + 6 – 2x = 6

Assume the third number = x

According to question

2 × 280 + x + 178.5 × 2 = 281 × 5

⇒ 560 + x + 357 = 1405

⇒ x + 917 = 1405

⇒ x = 1405 - 917 = 488

Let the third number be = x

∴ First number = 3x and second number =

According to the question.

⇒ 3x + + x = 3 × 121

⇒ = 3 × 121

⇒ = 3 × 121

∴ x = = 66

∴ Third number = 66

Required difference

= 3x – x = 2x = 2 × 66 = 132

Set the first, second and third no be F, S and T respectively,

Solving, we get F – T = 30.

Average of 20 numbers = 0.

∴ Sum of 20 numbers

= (0 × 20) = 0.

It is quite possible that 19 of these numbers may be positive and if their sum is a, then 20th number is (– a).

Sum of the remaining two numbers

= (3.95 × 6) – [(3.4 × 2) + (3.85 × 2)]

= 23.70 – (6.8 + 7.7)

= 23.70 – 14.5 = 9.20

∴ Required average

=

Sum of 10 numbers = 402

Corrected sum of 10 numbers

= 402 – 13 + 31 – 18 = 402

Hence, new average