Boats and Streams Exercise 2

Let upstream speed = S_u kmph

and downstream speed = S_d kmph.

Then,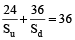 ...(1)

and 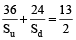...(2)

Adding (1) and (2), we get :

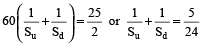...(3)

Subtracting (1) and (2), we get :

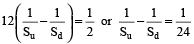....(4)

Adding (3) and (4), we get : 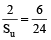or S_u = 8.

So,

⇒ S_d = 12.

∴ Speed upstream = 8 kmph,

Speed downstream = 12 kmph.

Hence, rate of current

= kmph = 2 kmph.

Speed of the boat in still water = 10 mph

Let the speed of the stream = x mph

Then, speed of boat with downward stream

= (10 + x) mph

Speed of boat with upward stream

= (10 – x) mph

Now,

or

⇒

⇒ 100 – x² = 48x

⇒ x² + 48 x – 100 = 0

⇒ x = 2 mph [x ≠ -50]

Let the speed of the boat in still water be x km/hr

Speed of the stream = 2 km/ hr

∴ Speed of the boat downstream

= (x + 2) km/hr

Speed of the boat upstream

= (x – 2) km/hr

⇒ 24x – 48 + 24x + 48 = 5(x² – 4)

⇒ 5x² – 48x – 20 = 0

=

∴ Speed of the boat in still water = 10 km/hr.

Let v_m = velocity of man = 48 m/min

Let v_c = velocity of current

then t₁= time taken to travel 200 m against the current.

i.e., ....(1)

and t₂ time taken to travel 200 m with the current

i.e., ....(2)

Given : t₁ – t₂ = 10 min

∴

⇒

⇒

⇒

Hence, speed of the current = 32 [since, v_c ≠ -72].

Let the speed of the stream be x km/h.

Then, upstream speed

= (15 – x) km/h.

and downstream speed

= (15 + x) km/h.

Now,

Checking with options, we find that x = 5 km/h.

Man’s speed in downstream

= .

∴ Man’s speed in still water

= 10 – 3 = 7 km/h

Man’s speed in upstream

= 7 – 3 = 4 km/h

∴ Required time

=

Suppose he moves 4 km downstream in x hours. Then,

Downstream speed

upstream speed

∴ Downstream speed = 8 km/h and upstream speed = 6 km/h

Rate of the stream

Time taken by the boat during downstream journey

=

Time taken by the boat in upstream journey

=

Average speed

= mph

Let speed of the boat in still water be x km/h and speed of the current be y km/h.

Then, upstream speed = (x – y) km/h

and downstream speed = (x + y) km/h

Now, …(i)

and …(ii)

Solving (i) and (ii), we have

x = 10 km/h and y = 4 km/h

Let the speed of the boat in still water be S kmph. Then,

Downstream speed = (S + 3) kmph,

Upstream speed = (S – 3) kmph.

⇒ 2S + 6 = 3S – 9

⇒ S = 15 kmph.

Downstream speed = (14 + 4) km/h = 18 km/h.

Upstream speed = (14 – 4) km/h = 10 km/h.

Let the distance between A and B be d km. Then,

⇒ d = 180 km.

Speed of the aeroplane against the wind = (320 – 40) = 280 km/h

Let the distance be x km. Therefore,

Again, speed of the aeroplane with wind = (320 + 40) = 360 km/h

Time taken by aeroplane with wind = 630/360 × 60 = 105 min

Let the man’s upstream speed be S_u kmph and downstream speed be S_d kmph. Then,

Distance covered upstream in 8 hrs 48 min.

d = Distance covered downstream in 4 hrs.

∴ Required ratio

=

= = 8 : 3.

Let the speed of the boatman be x km/hr and that of stream by y km/hr. Then,

⇒ 12x – 12y = 4x + 4y

⇒ 8x = 16y

⇒ x = 2y

Now

⇒ 45 + 135 = 60 y ⇒ 180 = 60y

⇒ y = 3km/hr.

Let the speed of the stream be x km/hr and distance travelled be S km. Then,

and

⇒ 108 – 9x = 72 + 6x

⇒ 15x = 36

Total distance covered = 2 × 91 km = 182 km

Time taken = 20 hours

∴ Average speed

=

Let the speed of flow of the river = x km/hr. then,

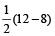Hence, rate of flow of the river = 3 km/h